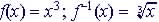
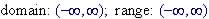
by Examples
Expanded Syllabus
| Chapter 3 : Functions
|
College
Algebra by Examples Expanded Syllabus |
| 3.1 Functions and Function Notation
A circle is not a function: A parabola is a function: |
Vertical Line Test: (Example
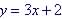 is a function)
is a function)
If a vertical line passes through a graph throughout its domain only at one point then that graph is a function. Domain: The possible values of x Range: The possible values of y One-to-one Functions: Passes the Horizontal Line test |
| 3.2 Quadratic Functions (parabolas)
|
The function 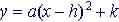 is a parabola (
is a parabola (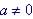 ) and the vertex is at (h, k).
(see Complete the Square)
) and the vertex is at (h, k).
(see Complete the Square)
The parabola or quadratic function as: 1. A maximum point is a < 0 2. A minimum point is a > 0
The function |
| 3.3 Polynomial and Other Functions
Symmetry about the y-axis:
Symmetry about the origin
when: |
Even function:
when 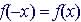 , usually powers of x are all even; symmetry about
the y-axis
, usually powers of x are all even; symmetry about
the y-axis
Example:
Odd function: when Then
|
| 3.4 Translation and Stretching Graphs
|
By Example: Let 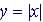 then
then
Horizontal Shift Right
by h :
Horizontal Shift Left by h :
Vertical Shift Up by h :
Vertical Shift Down by h : n
Vertical Expansion by factor of a :
Vertical Compression by factor of a : |
3.5
Rational Functions 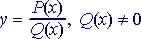
|
Rational Function: 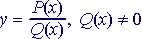
P(x) and Q(x) are polynomials To graph: Step 1: Check for symmetry
Step 2: Find and draw Vertical Asymptote(s): Q(x)
Step 3: Find and plot y-intercepts (when x = 0) and x-intercept(s) when P(x) = 0
Step 4: Find and draw horizontal asymptote (y as |
| 3.6 Operations on Functions
|
By Example: Let 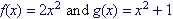
|
| 3.7 Inverse Functions
|
For a one-to-one
function 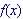 there exists an inverse function
there exists an inverse function 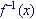 such that:
such that:
Both graphs are symmetrical about the line y = x The Domain of The Range of Example: Let For For |