College Algebra
by Example Series
|
Chapter
3.1 Functions and Function Notation
|
College Algebra by Example Series |
Key Concept: Understand the fundamental properties of function
Skills to Learn
1. Know how to recognize a function by its equation
2. Know the language use to represent a function
3. Know how to evaluate the Difference Quotient
4. Know how to recognize a function by is graph
5. Know the domain and range of some common functions
Function identification from equation or formula
| A function is a relationship that have only one value for y for each values of x |
Example: Is 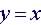 a
function? a
function?
Is a Function: 1 value of y for x: y = 2, x =2 |
Example: Is 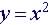 a
function? a
function?
Is a Function: 1 value of
y
for x: |
Example: Is 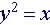 a
function? a
function?
Not a Function: Many values of x for y:
|
Example: Is 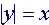 a
function? a
function?
Not a Function: Many values of x for y:
|
Example: Is 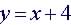 a
function? a
function?
Is a Function: 1 value of y for x: y = 6, x =2 |
Example: Is 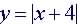 a
function? a
function?
Is a Function: 1 value of y for x: y = -2, x =2 |
Example: Is 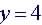 a
function? a
function?
Is a Function: A horizontal line |
Example: Is 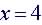 a
function? a
function?
Not a Function: A vertical line |
Functional Notation
| To
show
that y is a function of x write:
When x = 2, |
To
show
that y is a function of x write:
|
Example: Given 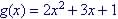
Evaluate g(x) for x = 2
So g(2) = 15 |
Example: Given 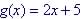
Evaluate g(x) for x = a+2
So g(a + 2) = 2a + 9 |
Example: Given 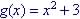
Evaluate g(x) for x = t + 1
So g(t + 1) = t2 + 2t + 4 |
Example: Given 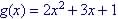
Evaluate g(x) for x = 0
So g(0) = 1 |
The Difference Quotient
Given
the function f(x) and 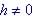 exactly, then the difference quotient is
defined as: exactly, then the difference quotient is
defined as:
|
Example: Evaluate
the difference quotient for 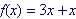
|
Example: Evaluate
the difference quotient for 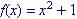
|
Vertical Line Test
| If a vertical line imposed on a graph intersects the graph only at one point for every value of x, then that graph is a function |
| A Function
|
A Graph
(not a function)
|
| A Graph
(not a function)
|
A Function
|
| Domain:
Possible values of x of a function
Range: Possible values of y of a function |
Example: Find
the
domain and range of 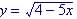 . .
Strategy: Cannot have the square root of a negative
number: So Solve: So domain is all values of To Find the range use
(e.g. Graphic Solution
|
Example: Find
the
domain and range of 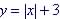 . .
Strategy: All values of x is possible since no value of x gives an impossible solution of y So domain is x equal all values of x or
Range: the |x| only gives positive numbers, the smallest value of y occurs when x = 0, since y = 0 + 3 = 3 and the highest values of y results when x is either a large negative or positive number. So range is Graphic Solution
|
Example: Find the domain
and range of 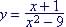 . .
Strategy: The denominator cannot be equal to 0; so find values of x that gives denominator = 0 and exclude them from the domain So So domain is
To find the range we solve the equation of x in terms of y or x=f(y)
(not readily seen, but difficult to solve for y) Graphic Solution ( Range is all values of y)
|
Example: Find the domain
and range of 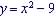 . .
No is no value of x that gives an impossible value for y So domain is x a all values of x.
To find the range we solve for x in terms of y
Cannot have the square root of a negative number so y > =
-9
since So range is
|
Domain and Range of Common Functions
Linear Function: 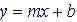
|
Absolute Value
Function: 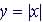
|
Domain: 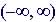
Range: |
Domain: 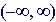
Range: |
Quadratic Function: 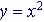
|
Square Root Value
Function: 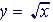
|
Domain: 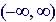
Range: |
Domain: 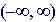
Range: |
| A Function
|
Domain and Range
|
|
|