College Algebra Home
Chapter  2.5 Proportion and Variation
Pindling
College Algebra  
by Example  Series

Key Concepts: Inverse Functions: How to determine if a function has an inverse, how to find the inverse of a function and how to graph both a function and its inverse.

Skills to Learn

1. Know how to determine if a function has an inverse:

(a) By one-to-one functions

(b) by horizontal line test

2. Know how to find the Inverse of a one-to-one Function

3. Know how to graph a functions and its

Inverse and observe symmetry about the line given by the function: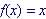

One-to-One Functions: are functions that do not have the same value of y (Range - Output Variable) for two or more values of x (domain - Input Variable). The Horizontal Line Test: If any horizontal line only crosses the graph of the function at one point then the function is one-to-one.

(a) is a one-to-one function

(b) is not a one-to-one function

(since x = -2 and x = 2 gives the same value for y of 4)

Inverse Functions:

Given a function ;

Its Inverse Functions is

A function and its Inverse is symmetrical about the function

Domain of a function is the Range of its Inverse

The Range of a function is the Domain of its Inverse

Determine if a function is a one-to-one function

Example 2. Is 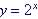a one-to-one function?

Yes - No 2 values of x have same y value

 Example 3. Is 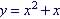a one-to-one function?

No - Several values of x has same value for y
Example 4. Is 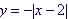a one-to-one function?

No - Several values of x has same value for y

 Example 4. Is 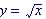a one-to-one function?

Yes - No 2 values of x have same y value

Find the inverse of a function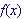

Example 6. Find the Inverse of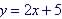

Step 1. Solve x in terms of y

So

Domain , Range (

Step 2. Substitute y with x and write as

Domain , Range (

Test: Is

Use

Graph of function and its Inverse

Example 7. Find the Inverse of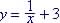

Step 1. Solve x in terms of y

So

Domain , Range (

Step 2. Substitute y with x and write as

Domain , Range (

Test: Is

Use

Graph of function and its Inverse

Example 8. Find the Inverse of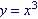

Domain all Range all

Step 1. Solve x in terms of y

So

Step 2. Substitute y with x and write as

Domain all, Range all

Test: Is

Use

Graph of function and its Inverse

Example 9. Find the Inverse of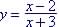

Domain , Range (

Step 1. Solve x in terms of y

So

Step 2. Substitute y with x and write as

Domain , Range (

Test: Is

Use

Graph of function and its Inverse