Chapter  3.3 Polynomial and Other Functions

Pindling College Algebra   by Example  Series

Key Concept: Know how to recognize the various shapes of n-th degree polynomials and be able to sketch a graph of their functions

Skills to Learn

1. Know the basic shapes polynomial of degrees 1, 2, 3, 4, 5 and 6

2. Know how the graph polynomial functions taking advantage of their symmetries

3. Know how to distinguish between even and odd functions

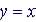
1-st Degree Polynomial:	2-nd Degree Polynomial:
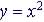
3-rd Degree Polynomial:	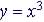4-th Degree Polynomial: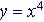

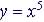
5-th Degree Polynomial:	6-th Degree Polynomial:
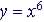
Odd-degree Polynomial - General Shape	Even-degree Polynomial - General Shape

Graphing Polynomial Functions

Steps in Graphing Polynomials: 1. Find any symmetries of the graph (about y-axis or about the origin) (a) symmetry about y-axis if f(x) = f(-x) (b) symmetry about the origin if f(-x) = -f(x) 2. Find intercepts (y-intercept when x = 0 and x-interects when y = 0) 3. Determine where graph ius above and below the x-axis 4. Plot a few points is needed 5. Draw the graph as a continuous curve

Example: Sketch the polynomial Step 1- Test for symmetry: (a) y-axis: (b) Origin: - see (a) So symmetry about the Origin Step 2 - Intercepts, y-int is y = 0 And x-intercepts are x = -2, 0, 2 Since Step 3 - Test is above or below for each domain Domain -5 -1 1 5 Test below above below above + / -

Step 5 Sketch Polynomial

Example: Sketch the polynomial Step 1- Test for symmetry: (a) y-axis: (b) Origin: - see (a) So symmetry about the y-axis Step 2 - Intercepts, y-int is y = 1 And x-intercepts are x = -1, 1 Since and Step 3 - Test is above or below for each domain Domain -5 0 5 Test above above above + / -

Step 5 Sketch Polynomial

Example: Sketch the polynomial Step 1- Test for symmetry: (a) y-axis: (b) Origin: - see (a) So no symmetry Step 2 - Intercepts, y-int is y = 1 And x-intercepts are x = 1 Since Step 4 - Plot a few points x -1 0 1 y 2 1 0

Step 5 Sketch Polynomial

Odd and Even Functions

Even Functions have graphs that are symmetrical about the y-axis So Odd Functions have graphs that are symmetrical about the origin So

Check if Even or Odd Function	Check if Even or Odd Function
Check if Even or Odd Function (not)	Check if Even or Odd Function
Check if Even or Odd Function	Check if Even or Odd Function (not)
Check if Even or Odd Function	Check if Even or Odd Function