Chapter
1.3 Quadratic
College Algebra
by Example Series
|
Chapter
1.3 Quadratic
|
College Algebra by Example Series |
Key Concept: Understand the Quadratic Equations, its roots and the interpretations of its various properties.
Skills to Learn:
1. Recognized forms of the Quadratic Equations
2. Convert all forms to Standard Form (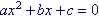
, where a, b, and c are real numbers and 
):
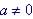A. Zero Form: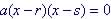 
B. Vertex Form: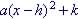 
, where (h,k) is the vertex
3. Learn how to complete the squares
4. Learn how to extract valuable information from the Quadratic Equations using the Completing the Square Algorithm.
5. Learn how to determine the nature of the roots of the Quadratic Equations
from examining its Discriminant (Given the Quadratic Equation in its Standard
form, its discriminant is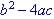 
)
| Discriminant | Nature of solution |
|
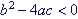
No real solution |
|
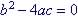
One real solution |
|
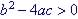
Two real solutions |
Example 1 - Solve for x in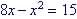 
| Standard Form: not in
the standard form so:
|
Solve by factoring:
Note: either So x = 3 and x = 5
|
| Completing the Square
The vertex is (4, -1)
Now can solve for x
|
Graphical Solution - Graph the function
|
| Quadratic Formula
For So the root, x = x =
So x = |
The Discriminant
The discriminant is Since the discriminant is positive (a, b, c are real numbers), then The solutions check as being Unequal real numbers |
Example 2 - Solve for x in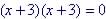 
| Already in Factored / Zero
Form: not in standard form but Zero Form with solution of x = 3
When both factors give the same value for x, the vertex is touching the x-axis. |
Standard Form (Expand
factors)
So , where a = 1, b = 6 and c = 9 |
| Completing the Square
- note Vertex is (-3, 0)
Now can solve for x
|
Graphical Solution - Graph the function
|
| Quadratic Formula
For So the root, x = x =
So x = -3
|
The Discriminant
The discriminant is Since the discriminant is zero (a, b, c are real numbers), then The solutions check as being Equal real numbers |
Example 3 - Solve for x in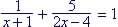 
| Standard Form: not in
standard form
Use (x+1)(2x-4) has common factor
|
Zero Form
So
So |
| Completing the Square
Vertex is Now can solve for x
|
Graphical Solution - Graph the function
|
| Quadratic Formula
For So the root, x = x =
So
|
The Discriminant
The discriminant is Since the discriminate is positive (a, b, c are real numbers), then The solutions check as being Unequal real numbers |
Example 4 - Solve for x in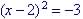 
| Standard Form: not in
standard form
However Expand to find standard form:
|
Zero Form
Factor: There is no factors of 7 that adds to -4 so no ready solution for the equation. |
| Completing the Square
(Purpose of completing the square is to put in Vertex Form, and since already in that form no more work is needed but to solve for x. So And |
Graphical Solution - Graph the function
No real solution; no value of x when y =0.
|
| Quadratic Formula
For So the root, x = x =
Since no real number with |
The Discriminant
The discriminant is Since the discriminate is negative (a, b, c are real numbers), then The solutions check as being No real number solution |
(multiply by -1 to make a +)
(now in standard form)
is Zero Form
or 
(next group x terms)
(complete the square)
(Vertex Form)
, 
, So x = 3 and 5
, and find x when y = 0 (x-axis)
, a = 1, b = -8 and c = 15
where
and 
(next group x terms)
(complete the square)
(Vertex Form 
)
, So 
, So x = - 3 
, and find x when y = 0 (x-axis)
, a = 1, b = 6 and c = 9
where
next factor
and 
(next group x terms)
(next make coefficient of x2 = 1)
(complete the square)
(complete the square)
(Vertex Form 
, 
, 
, So 
and
(next and find x when y = 0 (x-axis)
, a = 2, b = -9 and c = -5
where
is Vertex Form
(standard form)
, there is no real number with the square
root of a negative number so no real solution exist for this equation.
, a = 1, b = -4 and c = 7
where
, no real solution exist.