College Algebra
by Example Series
|
Chapter
3.5 Rational Functions
|
College Algebra by Example Series |
Key Concepts: Understand rational functions, their asymptotes and properties for graphing them
Skills to Learn
1. Know the basic features of a simple rational function: e.g. Average Hourly Cost
2. Know how to determine the domain of rational functions
3. Know how to find the vertical asymptotes of rational functions
4. Know how to find the horizontal asymptote of rational functions
5. Know how to graph rational functions
6. Know how to graph missing point on a graph
Definition of rational function
| A rational
function, r(x) is the ratio of two polynomials, P(x) and Q(x):
|
Basic Properties of Rational Functions
| Example 1. If the average
cost is the total cost, C divided by the number of items, n and the total
cost is C = P(n), where
P(n) = 2.25n + 5 show the following: (a) Formula for average cost:
(b) What is the average cost when 10 items are sold? So n = 10 and (b) Find n to give and average cost of 5.
So |
(e) Graph the rational
function
|
Domains of Rational Functions
Example 2. Find the
domain of the rational function 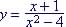
Note: the domain of a rational function is determined by the
restriction imposed by the denominator; here
And denominator is not equal to 0 when x = 2 and -2
Since So for the domain Values of x within |
Example 3. Find the
domain of the rational function 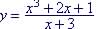
Note: the domain of a rational function is determined by the
restriction imposed by the denominator; here
And denominator is not equal to 0 when x = -3
Since So domain is all x except
Values of x within |
|
Example 4. Find the domain for Note: the domain of a rational function is determined by the
restriction imposed by the denominator; here
And denominator is not equal to 0 when x = -1, 0 and 1
Since So domain is Values of x within |
Example 5. Find the domain for Note: the domain of a rational function is determined by the
restriction imposed by the denominator; here
And denominator is not equal to 0 when x = - ½ and 3
Since So domain is Values of x within |
Vertical and Horizontal Asymptotes of Rational Functions
| Vertical
Asymptotes are found at values of x for which the r(x) gives the denominator
= 0.
So for Horizontal Asymptotes: Take the ratio of the highest degrees of P(x) and Q(x) and if (1) The degree of
(2) The degree of (there is a slant asymptote, i.e. The asymptote is a linear function)
(3) The degree of P(x) is a and the coefficient of
Q(x) is b, then the Horizontal Asymptote, HA = |
Example 6. Find the
asymptotes for 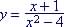
VA at HA at y = 0:
|
Example 7. Find the
asymptotes for 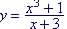
VA at No HA since
|
Example 8. Find the
asymptotes for 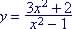
VA at HA at y = 3:
|
Example 9. Find the
asymptotes for 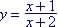
VA at HA at y = 1, since
|
Example 10. Find the
asymptotes for 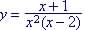
VA at HA at y = 0,
|
Example 11. Find the
asymptotes for 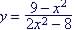
VA at HA at y = -½ , since
|
Note: Slant Asymptotes to be shown in class.
Graphing Rational Functions:
| Steps in
Graphing Rational Functions:
1. Check for symmetry: (a) Symmetry about y-axis
if (b) Symmetry about the origin if 2. Find the vertical Asymptotes: VA are x values when Q(x) = 0
3. Find the Horizontal Asymptotes: HA given the ratio of highest degrees of P(x) and Q(x): (1) When degree of Q(x) > P(x): HA = 0 (2) When degree of P(x) > Q(x): There is no HA (however slant asymptote) (3) When degree of P(x) = Q(x): HA = a, where a is the ratio of the coefficients of the highest degree of P(x) / Q(x) 4. Find the y-intercept: value of y when x = 0
5. Find the x-intercept(s): values of x when P(x) = 0
6. Plots a few point: within the domains given by the VA. |
|
Example 12. Graph (1) Symmetry about y-axis (even powers) (2) VA at x = 0 (since (3) HA at y = 3 ( (4) y-intercept: when x = 0 , y = Undefined (so no y-intercept) (5) x-intercepts: x = -2 and 2 when y = 0, |
So graph is:
|
|
Example 12. Graph (1) No Symmetry about y-axis or origin (2) VA at x = 0,-2, 2, since (3) HA at y = 0 ( (4) y-intercept: when x = 0 , y = Undefined (so no y-intercept) (5) x-intercepts: x = -3 and 1 when y = 0, |
So graph is:
|
|
Example 13. Graph (1) Symmetry about y-axis (even powers) (2) VA at x = -½ , ½, since (3) HA at y = ¼ ( (4) y-intercept: when x = 0 , y = 1 (5) x-intercepts: x = -1 and 1 when y = 0, |
So graph is:
|
Graphs with Holes or Missing point - No x or y-values
| Holes are missing points in
rational functions where both P(x) and Q(x) share the same factor
The hole is the point for the root of that common factor: Example 15: for the rational function
|
Graph of function with hole:
|
| Example 16. Grpah with
hole at x = 1
(x -1)
|
Example 16. Grpah with
hole at x = 0
Common factors of (x + 3) and (x - 5)
|