Chapter  3.2 Quadratic Functions

Pindling College Algebra   by Example  Series

Key Concept: Know the basic properties of a quadratic function and how to find its vertex and use these properties to find solution to real world applications

Skills to Learn:

1. Know how to graph quadratic functions (2nd degree polynomials)

2. Know how to find the vertex of a quadratic function

3. Know how to solve quadratic problems dealing with areas

4. Know how to solve quadratic problems dealing with revenue

Graphing Quadratic Functions

Graph the function 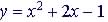Example: for x = 4: x y (x, y) -4 7 (-4, 7) -3 2 (-3, 2) -2 -1 (-2, -1) -1 -2 (-1, -2) 0 -1 (0, -1) 1 2 (1, 2) 2 7 (2, 7) 3 14 (3, 14) 4 23 (4, 23) Vetrex is (-1, -2) minimum point ( ) The y-intercept is (0, -1)

Graph of the Quadratic Function

Graph the function 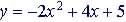Example: for x = 4: x y (x, y) -4 -43 (-4, -43) -3 -25 (-3, -25) -2 -11 (-2, -11) -1 -1 (-1, -1) 0 5 (0, 5) 1 7 (1, 7) 2 5 (2, 5) 3 -1 (3, -1) 4 -11 (4, -11) Vetrex is (1, 7) maximum point, ) The y-intercept is (0, 5)

Graph of the Quadratic Function

Finding the Vertex of Quadratic Functions

Find the vertex of the quadratic (or parabola) 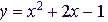. By Formula: Here a = 1, b = 2 and c = -1 So vertex is So vertex is (-1, -2)

By Completing the Square: 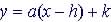So vertex is (-1, -2)

Find the vertex of the quadratic (or parabola) By Formula: Here a = -2, b = 4 and c = 5 So vertex is So vertex is (1, 7)

By Completing the Square: 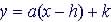So vertex is (1, 7)

Quadratic Application of Area and Revenue

Find the maximum area of a rectangular with width = x and length = 100 less 2 times the width. Area = Length x Width = (100 - 2x)x So Area = This is a quadratic or parabola so vertex is , where a = -2, b = 100 and c = 0 Also can complete the square to get (h, k)

Find the maximum revenue if price per unit n is given by the formula 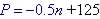Remember that revenue, R = Price times total unit sold, n. So This is a quadratic or parabola so vertex is , where a = -0.5, b = 125 and c = 0 So the maximum revenue if $7,812.50 after 125 units are sold.