Chapter 0: Basic Algebra Review
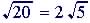
by Examples
Chapter Summary
| Expanded Syllabus Chapter 0: Basic Algebra Review
|
College
Algebra by Examples Chapter Summary |
| 0.1 Sets of Real Numbers
|
|||||||||||||||||||||||||||||||||||||||
| 0.2 Integer Exponents and Scientific Notation
|
Properties of Exponents:
|
||||||||||||||||||||||||||||||||||||||
| 0.3 Rational
Exponents and Radicals
: m and n are positive integers
|
: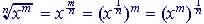
(e.g.
|
||||||||||||||||||||||||||||||||||||||
| 0.4 Polynomials Monomial: Binomial: Trinomial: The Conjugate of a + b is a - b
The degree of monomial (sum of exponents of variables) |
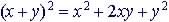
Rationalize Numerator / Denominator (a) (b) |
||||||||||||||||||||||||||||||||||||||
| 0.5 Factoring Polynomials
|
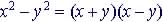
|
||||||||||||||||||||||||||||||||||||||
| 0.6 Algebraic Fractions
If |
If 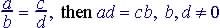
|
||||||||||||||||||||||||||||||||||||||