Department of Mathematics

Pindling Basic Algebra   by Example Series

Skills to Learn

1. Learn how convert between Rational Exponents and Radicals

2. Know the basic properties of Radicals

3. Know how to simplify Radicals

4. Know how to compute the sum and difference of Radicals

5. Know how to compute the product of Radicals

6. Know how to rationalize the denominator (removed radicals)

Conversion Between Rational Exponents and Radicals

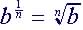, stated as the n-th root of b Examples: (1) , the square root of 13 or (2) , the 4-th root of a or

Rational Exponent	Radical
(1)
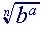
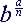
(2)
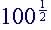
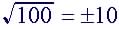
(3)
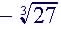
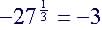
(4) 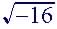, not a real number	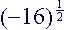, not a real number
(5)
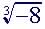
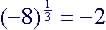
(6)
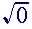
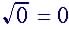
(7)
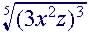
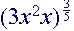
(8)
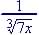
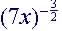
(9)

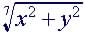
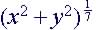
Properties of Radicals

Properties	Examples
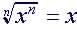
	(a) 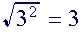(b)
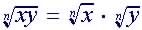
	(a) (b)
	(a) (b)

Simplifying Radicals

Strategy: remove as many terms from the radical and eliminate the radical is possible.

Example 10. Simplify Strategy: look for cube root factors and remove from radical Solution is	Example 11. Simplify Strategy: group terms under radical and find and remove square root factor(s) from radical Remember:
Example 12. Simplify Strategy: look for cube root factors and remove from radical	Example 13. Simplify Strategy: look for 5-th root factors and remove radical

Sums and Differences

Strategy: Combine / group like terms and evaluate

Example 14. Simplify Strategy: Group terms.

Example 15. Simplify Strategy: group like terms

Multiplication and Divisions

Strategy: Multiply or divide like terms and simplify

Example 16. Simplify Strategy: Expand via multiplication radicals.	Example 17. Simplify Strategy: Expand keeping terms together So
Example 18. Simplify Strategy: Expand keeping terms together So	Example 19. Simplify 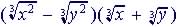Strategy: Expand keeping terms together

Rationalizing the Denominator

Strategy - Eliminate the radical from the denominator by multiplying both the numerator and denominator by a suitable
factor that will leave the denominator free of radicals.

Remember:

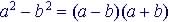or	Example (note )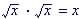
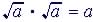
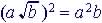
	45

Examples of Rationalizing Denominator

Example 20. Rationalize denominator for 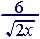Strategy: multiply numerator and denominator by So	Example 21. Rationalize denominator for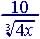 Strategy: multiply numerator and denominator by So
Example 22. Rationalize denominator for Strategy: rationalize with So	Example 23. Rationalize denominator for , If a = 1 and Strategy: rationalize with Note: If Then: