Department of Mathematics

Pindling Basic Algebra   by Example Series

Key Concept: Know the basic meaning and properties of a polynomial so as to perform basic operations with
polynomials

Skills to Learn

1. Know how to identify polynomials (monomials, binomials, and trinomials)

2. Know how to add and subtract polynomials

3. Know how to multiply and divide polynomials

4. Know how to find the Conjugate Binomials

Definitions of Polynomials

Polynomials (a monomial or the sum of monomials) with whole number exponents
Monomials (a product of one or more variables)	Binomials (a polynomial with 2 terms)	Trinomials (a polynomial with 3 terms)
-5x3 (degree 3, coefficient -5)	2x5 + 3x2 (degree is 5)	2x5y2 + 3x2 + 5x (degree is 7)
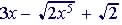
15x3y (degree 4, coefficient 15)	-3x3 - 4y4 (degree is 4)	(degree is 5)
3a2bc2 (degree 5, coefficient 3)	3x2y4 + 3xy (degree is 6)	3x2y2 + 5xy2 + 2x (degree is 4)

Add and Subtract Polynomials

Example: Add Remove parentheses and group like terms	Example: Add 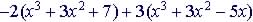Remove parentheses and group like terms
Example: Subtract Remove parentheses and group like terms	Example: Subtract Remove parentheses and group like terms

Multiply Polynomials

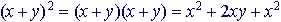
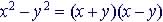
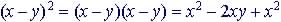
	Foil method of multiplication (a + b)(c + d) = ac +ad +bc +bd

Example: Multiply 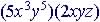Remove parentheses and use commutative property	Example: Multiply 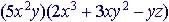Expand (distributive property) (no like term so finish)
Example: Multiply 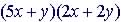Foil (then combine xy terms) (then factor out 2)	Example: Multiply 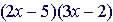Foil

Dividing Polynomials

Example: Divide Move exponents in denominator to numerator	Example: Divide
Example: (text book gives better example using sign) Note: So Note: So Answer is	Example: (text book gives better example using sign) Note: So Note: So Answer is

Conjugate Binomials

The conjugate binomial: the conjugate of (a + b) = (a - b) and the conjugate of (a - b) is (a + b) Example: the conjugate of

Used to rationalize denominators (also numerators)

Conjugate Binomial

Example: Rationalize The conjugate of and So So	Example: Rationalize denominator for Conjugate of So
Example: Rationalize the numerator Conjugate: So So	Example: Rationalize the denominator Conjugate of So Or