Programs Used: Correlation and Regression - Graphs
 

Review: r is correlation coefficient: When r = 0 no relationship exist, when r is close to 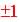 there is a high degree of correlation. Coefficient of determination is r2, and it is: (a) The ratio of the explained variation to the total variation: SSR/TSS (SSR - sum of square for regression and TSS - total sum of squares) (b) A r2 of 0.81 means that 81% of the variation is explained by the regression line or (c) A r2 of 0.81 means that 81% of the variability in y is explained by x.

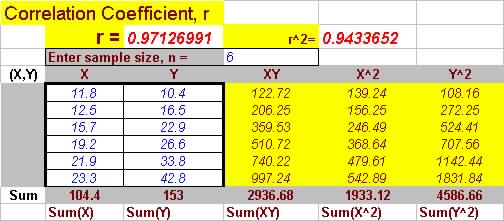
Question 1. From the following table first determine the degree of linear correlation
(find and interpret the correlation coefficient and coefficient of determination) and find the line that best fit the data.
 

y	10.4	16.5	22.9	26.6	33.8	42.8
x	11.8	12.5	15.7	19.2	21.9	23.3

Solutions:
The correlation coefficient and coefficient of determination are:r = 0.9713 and r²=0.9434

Since r is close to 1 it means that there is a strong linear relationship between x and y and from
r², 94% of the variation in y can be explained by the variation in x.

From statistics program:
 

The regression line of best fit line is y=-15.474 + 2.355 x
 

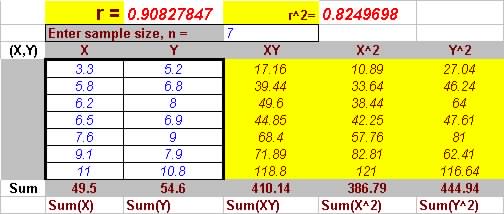
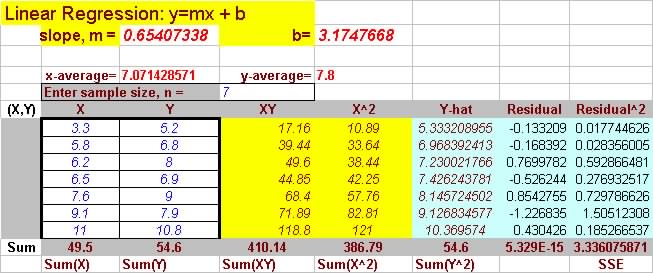
Question 2. Draw a scatter plot of the following data and after determining its degree of correlation
(find r and r²), find the line of best fit for predicting the prime lending rate (y) from the inflation rate (x).
 

Inflation rate (ordered data)	Prime lending rate
3.3	5.2
5.8	6.8
6.2	8
6.5	6.9
7.6	9
9.1	7.9
11	10.8

Solutions:
 

The correlation coefficient , r = 0.9083 And the coefficient of determination, r2= 0.825 So 82.5% of the variation in prime lending rate can be explained by the inflation rate. The linear regression line is: y=0.654x + 3.175 See program summaries below:

Correlation program summary
 

Regression program summary
 

Question 3. (3/11) Education and crime rate ratings for selected US cities are given below:
Education rating is an index for public/teacher ratio, academic options in higher education:
the higher the rating the better and other factors and crime is the crime rate per 100 people
.

City	Education (x) ordered data	Crime (y)
New York	30	25
Detroit	31	16
Los Angeles	32	20
Boston	35	12
Chicago	35	10
Washington, DC	36	13

(a) Draw a scatter diagram. Does there appear to be a linear relationship between education and crime rate?

(b) Compute and interpret the correlation coefficient and coefficient of determination

(c) Find and sketch the line of best fit for predicting crime rate from education rating.

(d) Estimate the crime rate for an education rating of 34.

Solutions:

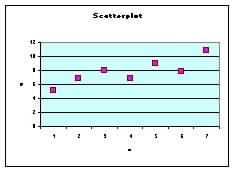
(a) Scatter plot
 

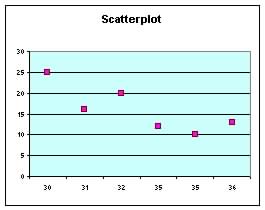
Note plot does not start at x=0

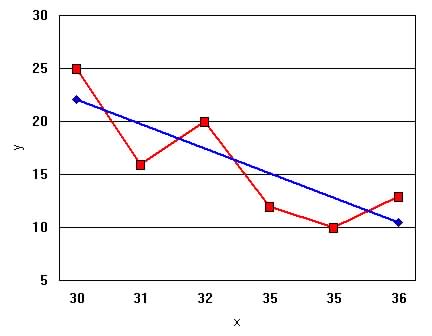
(c) Plot of regression line (in blue) Note plot does not start at x=0

Correlation coefficient, r (from program)
 

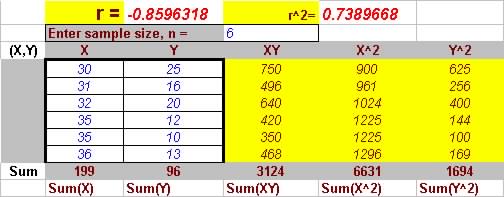
(b) So r = -0.86 suggesting that as x gets large y gets small (evident from the negative sign) from r2 = 0.739, 73.9% of the variation in y can be explained by x.

Linear Regression program summary
 

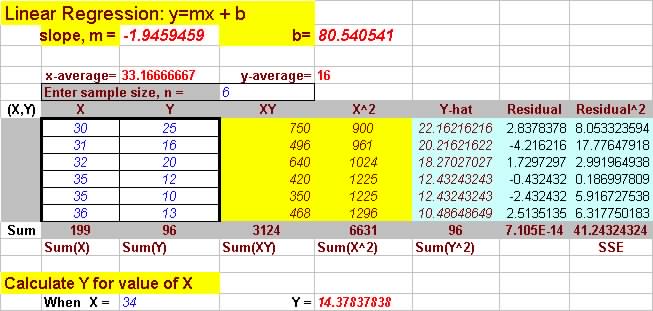
(c) Best fit line is y=-1.95x+80.54 (d) When x = 34, y = 14.38

Question 4. The data below summarized the relationship between number of employees (x)
and number of openings (y) at 11 Boston area hospitals.

x = 56,562  x² = 456,525,234  y = 2611  y² = 818,149  xy = 18,267,023

(a) Find the correlation coefficient, r

(b) Find the coefficient of determination and interpret its value.

Solution: n = 11

(a) The correlation coefficient is given by the formula: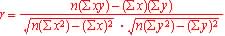 

So from data: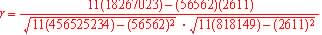 

So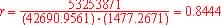

(b) The coefficient of determination, r² = 0.8444 = 0.713

This means that 71% of the variations in the number of openings can be explained by the linear relationship
between it and the number of employees.