|
|
|
|
| Introduction to Transformation
Given: f(x) g(x) = A f(B(x)-h) + D g(x) = +/-A f(+/-B(x)-h)+D h = horizontal shift: +h is shift to right; -h (x+h) is shift to left B = horizontal stretch: 0<B<1 is stretch; B>1 is compression -B = reflection about the y-axis A = vertical stretch: A>1 is stretch; A < 1 is compression -A = refection about x-axis D = vertical shift: +D is shift up ; -D is shift
down
|
| Order of Transformation
Given: f(x) g(x) = +/-A f(+/-B(x)-h)+D 1. h = horizontal shift 2. B = horizontal stretch / compression 3. -B = reflection about the y-axis 4. A = vertical stretch / compression 5. -A = refection about x-axis 6. D = vertical shift
|
1. Horizontal shift y = f(x-h)
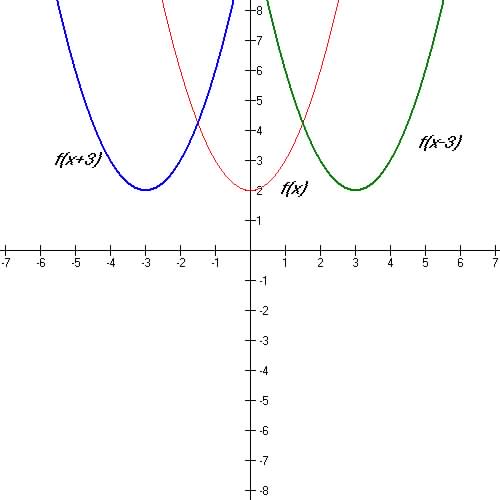 |
2. Horizontal stretch / compression y = fB(x)
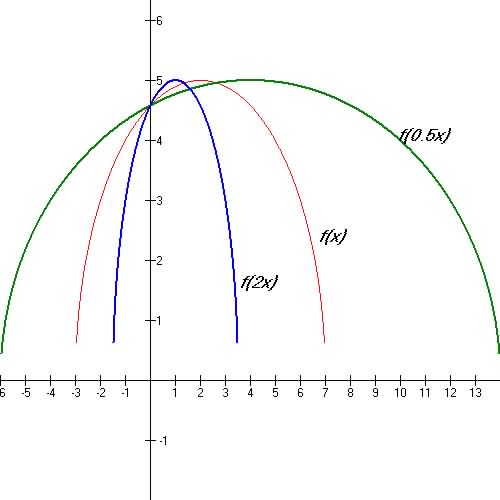 |
3. Horizontal reflection about y-axis: y=f(-x)
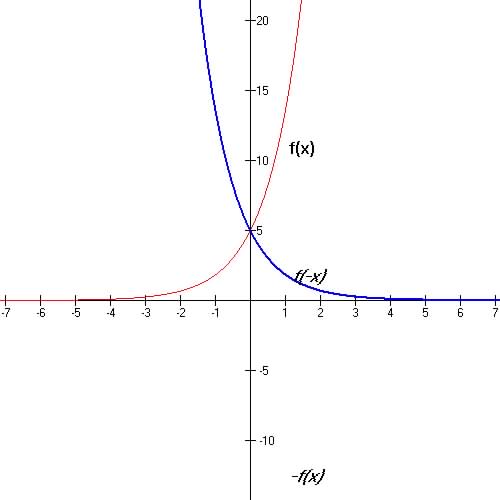 |
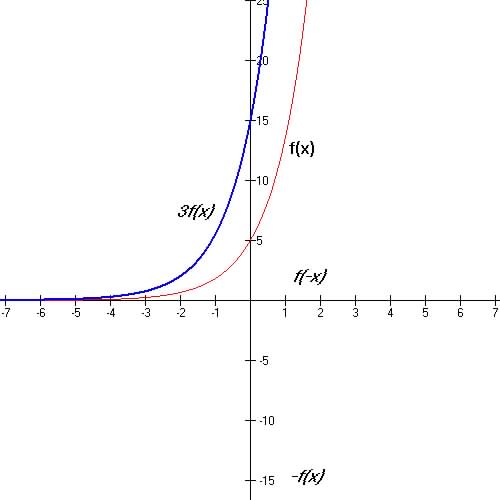
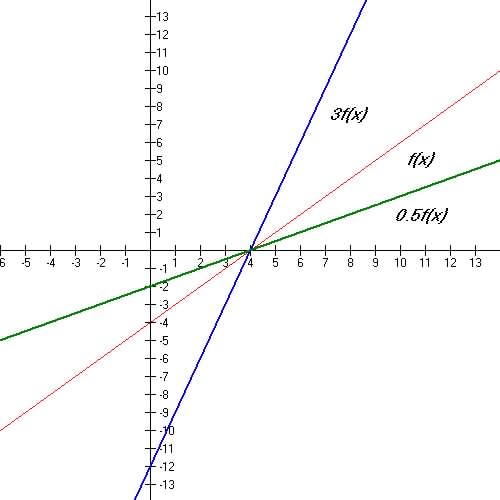
4. Vertical Stretch / Compression: y = A f(x)
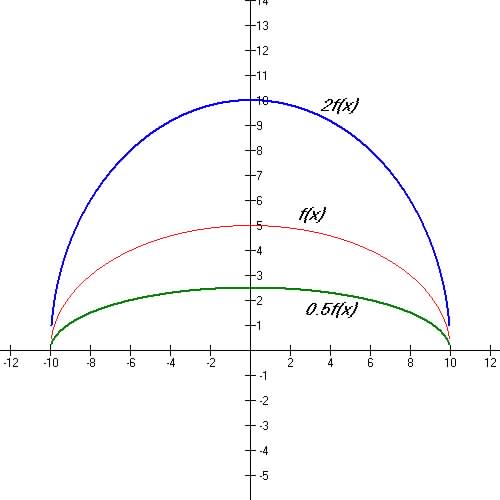 |
 |
 |
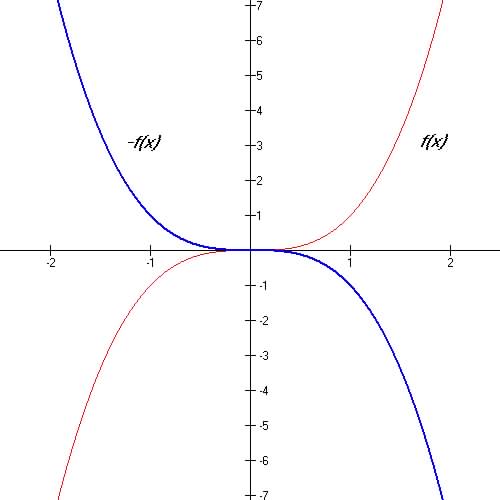
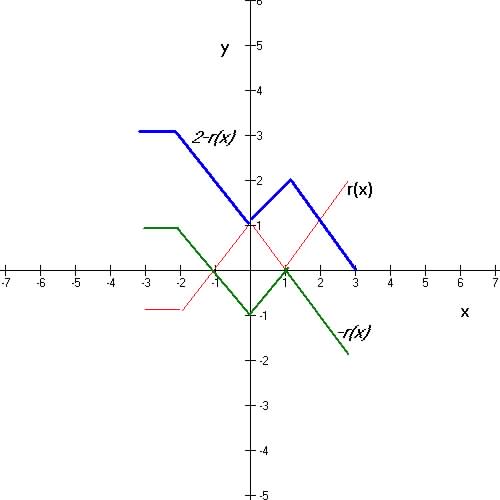
5 Vertical Reflection about x-axis (-A): y = - A f(x)
 |
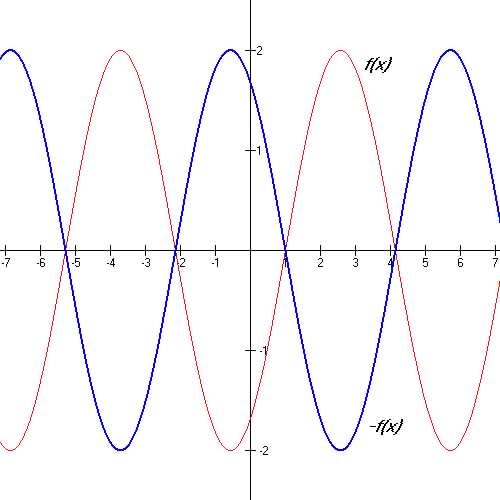
5. Vertical reflection example 2
 |
6.vertical shift: y = f(x) + D
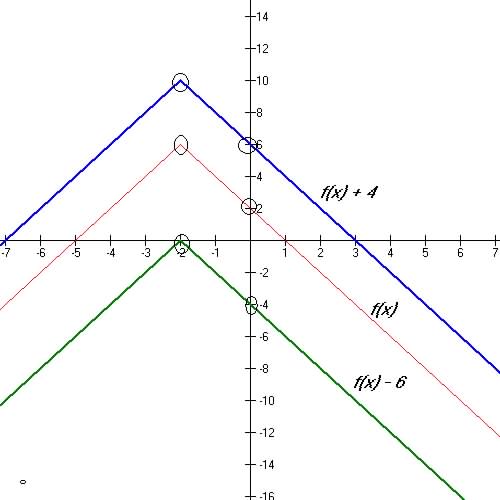 |
 |
Example 2
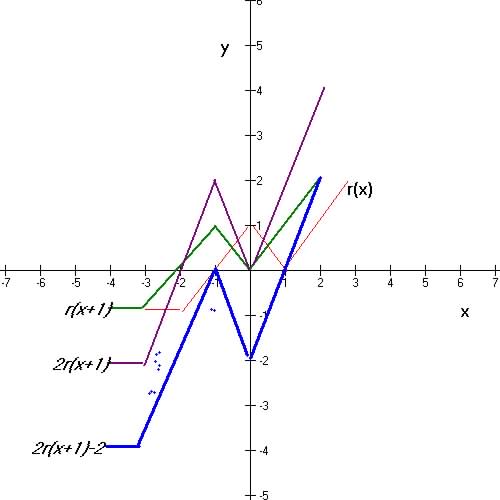 |
Example 3
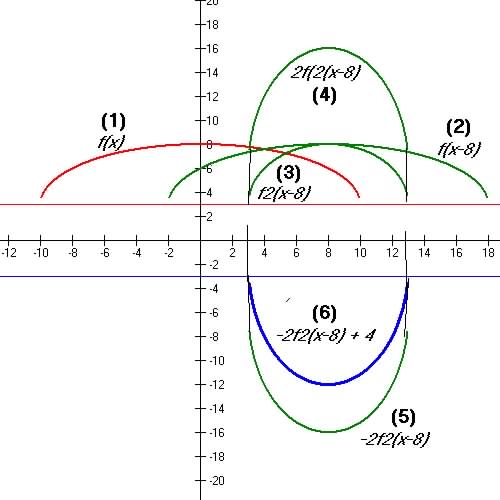 |