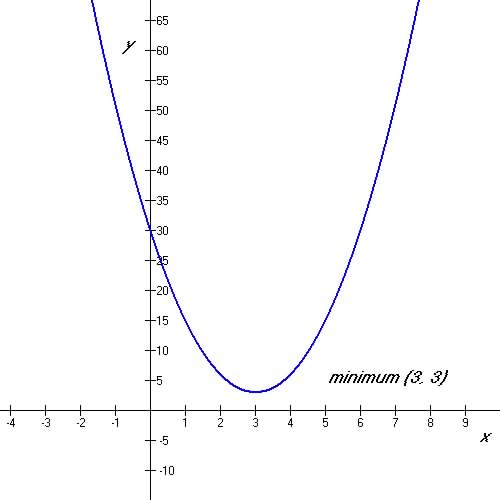
Question 1 Find a possible formula for the following graph drawn below:
 

Given 2 points of a quadratic function: y-intercept: (0, 30) and vertex (3, 3)

So use vertex form of quadratic: y = a(x-3)² + 3

Use point (0, 30): 30 = a(0 - 3)² + 3=9a + 3, 

So formula is : y = 3(x-3)² + 3

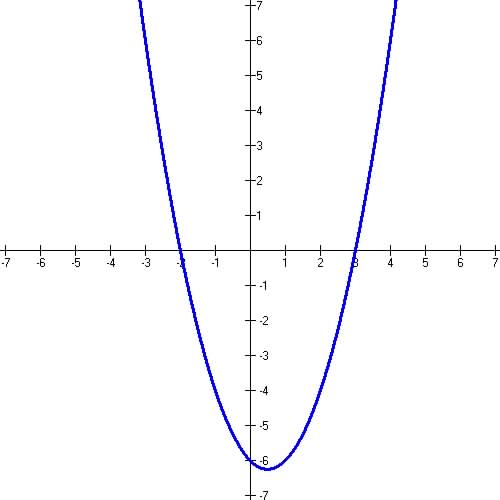
Question 2 - Sketch the graph of the quadratic function: y= x² - x - 6:
State its vertex, y-intercept, and zeros (points where graph crosses the x-axis)

Vertex:  So Minimum:

So y-intercept: (0, -6), zeros: (-2, 0) and (3, 0) from graph below

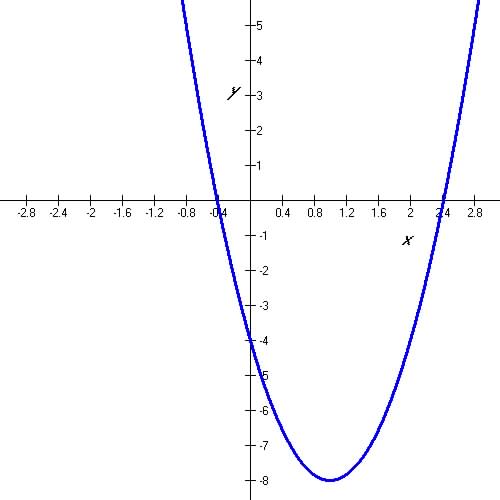
Question 3. Sketch the quadratic equation y = 4x² - 8x -4 and state its vertex, y-intercept
and zeros if any (points where graph crosses the x-axis)

(a) vertex form: (4x²-8x ) - 4 = 4(x² - 2x ) - 4 = 4(x² - 2x +1) - 4 - 4

y = 4(x-1)² -8, So vertex is (1, -8)

(b) y-intercept: when x = 0, y = -4:

(c) zeros, when y = 0: From graph:

(see quadratic formula solution below for more exact and more accurate solution)
  Quadratic formula: 

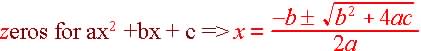
Since a = 4, b = -8 and c = -4

 
 

Zeros: x  -0.4 and 2.4

y - int : (0, -4)

minimum at ( 1 , - 8)

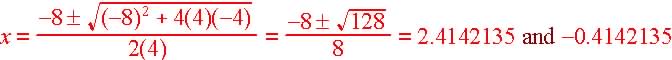
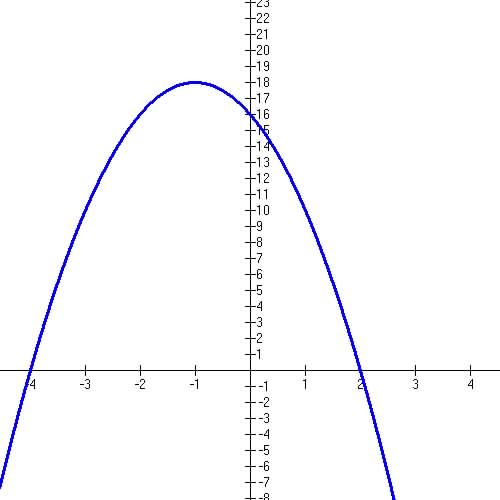
Question 4 - Show that  graph below has equation y = -2x2 - 4x +16
  (hint: use quadratic zeros formula and property of y-intercept)