General Statistics
Examples
Inference about 2 sample means and proportions.

Programs / Reference Tables       Hypothesis Worksheet
 

Question 1 (8.13) For the following data, complete the test at the 5% level of significance. Assume that the samples are independent.

(a) It was claimed that the mean of population A was not the same as the mean of population B.
 
  n s2
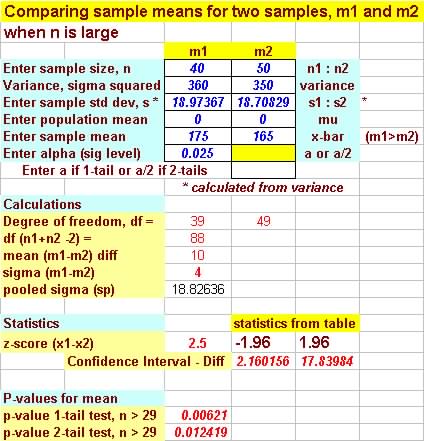
A 40 175 360
B 50 165 350

Solution:
 
Given: 

then critical value of 

Observed value

 Decision: RejectH0, since 2.5 > 1.96

and 

P-value = 2P( ) 

= 2(0.0062)= 0.0124

P-value < 0.05 

This is the results from the test - statistics Program:

(b) It was claimed that the mean of population A was larger than the mean of population B.
 
  n s2
A 35 400 210
B 35 395 105

Solution:
 
Given: 

then critical value of 

Observed value

 Decision: Do not Reject H0, since 1.33 < 1.65

and 

P-value = P( ) = 0.0918

P-value > 0.05 

(c) It was claimed that the mean of population A was less than the mean of population B.
 
  n s2
A 52 42 260
B 54 48 216

Solution:
 
Given: 

then critical value of 

(lower tail )

Observed value

 Decision: RejectH0, since -2 < -1.65

and 

P-value = P( ) = 0.0228

P-value < 0.05 

Question 2. (8.15) Summary information on the height of 57 alto and 66 soprano singers, all women, in the New York
Choral Society is given (8.15 of text). The vocal part is lower in pitch than soprano voice part.
 
  n s2
Alto (A) 57 65.39 7.02
Soprano (B) 66 64.12 4.75

Use a 5% level of significance to determine whether there is a difference in the population mean heights between alto and soprano singers.

(a) Use the classical approach (b) use the P-value approach.

Solution:
Given: 

then critical value of 

(2-tail test )

Observed value

 (a) Decision: RejectH0, since 2.875 > 1.96

(b) 

P-value = 2P( ) = 2(0.0020) = 0.0040

P-value < 0.05 

Question 3 (8.21)

(a) Do the following data support the belief that the mean of population A is different from the mean of population B?
Assume approximately normality for the populations, and compete the test using the 5% level of significance.

It was claimed that the mean of population A was not the same as the mean of population B.
 
Sample n s2
A 8 83 21
B 12 80 5

Solution: (Since sample size small use t-test )
 
Given: 

then critical value of 

(2-tail test )

Observed value

 (a) Decision: AcceptH0, since 1.72 < 2.365

(b) 

P-value = 2P( ) = 2(0.0513) = 0.1026

P-value > 0.05 

The data does not suggest the means are different.

(b) It was claimed that the mean of population A was larger than the mean of population B. Test at the 1% significance level.
 
  n s2
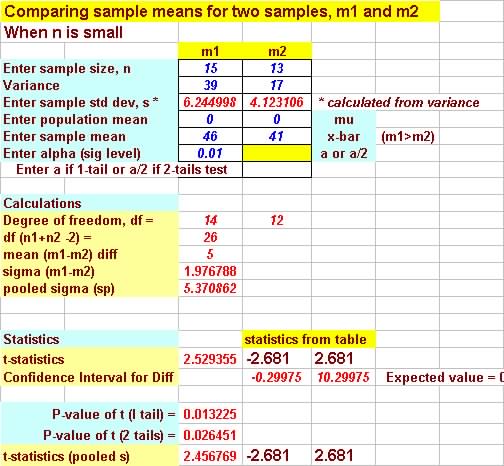
A 15 46 39
B 13 41 17

Solution: (Since sample size small use t-test )
 
Given: 

then critical value of 

(1-tail test )

Observed value

 (a) Decision: AcceptH0, since 2.53 < 2.681

(b) 

P-value = P( ) = 0.013

P-value > 0.01

The data does not suggest the means are different.

Results from Test Statistics Program:

(c) It was claimed that the mean of population A was less than the mean of population B. Test at the 10% significance level.
 
  n s2
A 10 180 70
B 7 200 340

Solution: (Since sample size small use t-test )
Given: 

then critical value of 

(1-tail test )

Observed value

 (a) Decision: Reject H0, since -2.68 < -1.440

(b) 

P-value = P( ) = 0.018

P-value < 0.01 

The data does suggest the mean A is less than mean B.

Question 4 (8.37)

In each of the following parts, assume independent samples. Note that n refers to sample size and x is the number of successes.

(a) It is claimed that proportion p1 and p2 for population A and B, respectively, are the same.
Consider the following information and test using the 5% level of significance.

It was claimed that the population proportion A was not the same as the population proportion B.
 
  n x
A 250 175
B 175 135

Solution: (Since proportion being compared and sample size large use z-score )
 
Given: 

then critical value of 

(2-tail test )

Observed value

 (a) Decision: AcceptH0, since 1.63 < 1.96

(b) 

P-value = 2P( ) = 0.1028

P-value > 0.05 

The data does not suggest the proportions are different.

(b) It is claimed that proportion p1 for population A is larger than proportion p2 for population B,
Consider the following information and test using the 10% level of significance.

It was claimed that the population proportion A is larger than the population proportion B.
 
  n x
A 375 195
B 325 150

Solution: (Since proportion being compared and sample size large use z-score )
 
Given: 

then critical value of 

(1-tail test )

Observed value

 (a) Decision: RejectH0, since 1.63 < 1.96

(b) 

P-value = P( ) = 0.061

P-value < 0.10 

The data does suggest that proportions A is larger than proportion B.

(b) It is claimed that proportion p1 for population A is less than proportion p2 for population B,
Consider the following information and test using the 5% level of significance.

It was claimed that the population proportion A is less than the population proportion B.
 
  n x
A 425 175
B 400 205

Solution: (Since proportion being compared and sample size large use z-score )
 
Given: 

then critical value of 

(1-tail test )

Observed value

 (a) Decision: RejectH0, since 1.63 < 1.96

(b) 

P-value = P( ) = 0.061

P-value < 0.10 

The data does suggest that proportions A is small than proportion B.

Below is the results from the Test - Statistics Program:

Question 5. (8.41) In a case of Jackson v. Nassau County Civil Service Commission, 424 F. Supp.
1162, 1167 (E.D.N.Y. 1976), the following information was given concerning the results of an examination taken by job applicants:
 
  n x
Blacks  40 15
Whites 99 14

(a) Test the claim that the population proportion of blacks who pass is less than that of whites at the 2.5% level of significance.

(b) The "80% rule" says that a "substantial" disparity between groups can ordinarily be shown only when the data are significant i.e.,
lead to rejection of the null hypothesis) and the pass rate for the protected group (blacks in this case) is less than 80% of the pass rate
of the group with the highest pass rate. Do the data meet the requirement of the 80% rule?

Solution:

(a) Observed z = -2.40 and z-Table = -1.96 ( 1-tail test ) so Reject H0 since z-statistics = -2.40 < -1.96
or P-value = 0.0083 < alpha value of 0.025

(b) p-hat = 0.827 which is > 0.80, so data do not meet the requirement of the 80% rule.

From Program: