Programs Used: Permutation and Combinations - Joint Probability Table

Question 1.  Suppose that a lottery number is determined by selecting four digits in succession and recording each digit
when selected (Repeated digits are allowed). List the elements of the event where

(a) The digits 426 are the first 3 digits, in that order.

(b) The four digits consists of 4, 2, and 6 in the 1st three positions (not necessarily in that order) and 8 in the 4th position.

Solutions:

(a) The set of 4 digits with 426 as the 1st 3 digits is:

{4260, 4261, 4262, 4263, 4264, 4265, 4266, 4267, 4268, 4269} - set has 10 elements

(b) Set of 1st 3 digits being any of 4, 2, 6 and 8 in 4th place is: set has 6 elements

{2468, 2648, 4268, 4628, 6248, 6428}

Question 2.  A hospital administrator records a 0 if a patient has no medical insurance and a 1 if the patient does have medical insurance.
The administrator also records an A, B, C, D, or E, representing good, fair, poor, serious, or critical condition, respectively.

List the elements of the sample space S, and list the element of the event consisting of a selected patient.

(a) With no medical insurance and in serious or critical condition

(b) With medical insurance and not in critical condition

(c) In good or fair condition

(d) With medical insurance.

Solutions:

(a) With no medical insurance and in serious or critical condition

Set 0 or D = {0D, 0E}

(b) With medical insurance and not in critical condition

Set I and not E = {1A, 1B, 1C, 1D}

(c) In good or fair condition

Set A or B (so both 0 and 1) = {0A, 1A, 0B, 1B}

(d) With medical insurance.

Set 1 = {1A, 1B, 1C, 1D, 1E}

Question 3. Assume there is a 50-50 chance that a newborn child will be a boy. In a family of 4 children, find the probability that

(a) There are exactly two boys

(b) The oldest two children are boys

(c) All the children are girls.

(d) Not all the children are girls

Solutions:

Let B be event boy and G be event girl: Pr[B] = ½

Fundamental Principle of Counting - Each birth can be either a B or G so 2 ways and since 4 events or birth,

the sample space is of size = 2 x 2 x 2 x 2 = 16

(a) There are exactly two boys

Events with exactly 2 boys are: {BBGG, BGBG, BGGB, GBBG, GBGB, GGBB} = 6 in set

Pr[ exactly 2 boys] = 6 /16 = 3/8

(b) The oldest two children are boys

Events where the oldest two children are boys: {GGBB, BBBB, BGBB, GBBB}= 4 in set

So Pr[ oldest 2 are boys] = 4/16 = ¼

(c) All the children are girls.

Event all children are girls: {GGGG}

Pr[all girls] = 1/16

(d) Not all the children are girls

Pr[not all girls] = 1 - Pr[all girls] = 1 - 1/16 = 15/16

Question 4.  The following data represents the numbers of earned degrees conferred in the USA and Puerto Rico
for the years 1960. 1970 and 1980. The data values are in thousands.
 

Year	Bachelor's	Master's
1960	395	75
1970	833	209
1980	999	298

Is a degree recipient is selected by chance (assume 1 degree per recipient). Find the probability that the recipient

(a) Received a master's degree

(b) Received a degree in 1970

Solutions
 

Year	Bachelor's	Master's	Total
Y1960	395	75	470
Y1970	833	209	1,042
Y1980	999	298	1,297
Total	2,227	582	2,809

(a) Received a master's degree: Pr[Master] = 582/2809 = 0.2072

(b) Received a degree in 1970: Pr[Degree in 1970] = 1042/2809 = 0.3710

Question 5.  A card is selected randomly from a deck of 52 cards. Consider the events: A = ace, B = face card, and C = club.

(a) Verify that the only pair of mutually exclusive events is A, B.

(b) Use the addition Rule to find P(A or B).

Solutions:

(a) Two events are mutually exclusive if they both cannot occur at the same time:

Addition Rule: There is 4 ace cards and 12 face cards so Pr[A or B] = 4/52 + 12/52 = 16/52 = 4/13

Counting Method: The Pr[ace or face] = total ace and face / 52 = 16/52 = 4/13

Since by the counting method and simple addition rule Pr[ace and face] are equal we can assume that Pr[A and B] = 0,
so mutually exclusive

(b) Addition Rule: Pr[A or B] for mutually exclusive events = Pr[A] + Pr[B] = 4/52 + 12/52 = 4/13

Question 6. The following is the number of people voting in an election so find:
 

	A Voted	Did not vote
B Males	53,312	35,245
Females	60,554	36,573

(a) P(B) (b) P() (c) P( and )

Solutions:
 

	A Voted	Did not vote	Totals
B Males	53,312	35,245	88,557
Females	60,554	36,573	97,127
Totals	113,866	71,818	185,684

(a) Pr[B] = 88557/185684 = 0.4769

(b) Pr[] = 71818/185684 = 0.3868

(b) Pr[( and )] = 36573/185684 = 0.197

Question 7. Suppose that the probability that a child produced by a couple will have a particular disease is 0.10.
If they plan to have four children, what is the probability that one or more children will have the disease?

Solution - Probability of "At least One"

The question is what is the Pr[of one or more] or Pr[at least one]

"At least One" is the opposite of "None", so if event A is the probability of having the disease:

We have Pr[A] = 0.10 ( given) and so Pr[] = 1 - Pr[A] = 0.90

Or the Pr[ at least one] = 1 - Pr[none]

Pr[none] for one a child is 1 - 0.10 = 0.90 and
the Pr[none for all 4 children] = Pr[] x Pr[] x Pr[] x Pr[] = 0.90 x 0.90 x 0.90 x 0.90 = 0.6561

So Pr[ at least 1] = 1 - Pr[] = 1 - 0.6561 = 0.3439

Question 8. A business employ 600 men and 400 women. Five percent of the men and
10% of the women have been working there for more than 20 years. If an employee is selected by chance,
what is the probability that the employee is male, given that the length of employment is more than 20 years?

Solution:

The proportion or probability of men at the business is 600/1000 = 0.6 so Pr[male] = 0.6

5% or 5/100 or 0.05 of the men have been working over 20 years, so Pr[male and >20 yrs] =0.05

So Pr[male given worked over 20 years] is a conditional probability statement:

Pr[male|worked > 20 yrs] = Pr[male and worked > 20 yrs] / Pr [worked > 20 yrs]

Or Pr[male| worked >20yrs] = Number males / Number Worked > 20yrs

Pr[worked > 20yrs] = 5% + 10% = 0.15

So Pr[male|worked > 20 yrs] = Pr[male and worked > 20 yrs] / Pr [worked > 20 yrs] = 0.05 / 0.15 = 0.3333

???

Question 9. A change was proposed in the mathematics curriculum at a college.
The mathematics majors were asked whether they approved of the proposed change. The results of the survey follow.
 

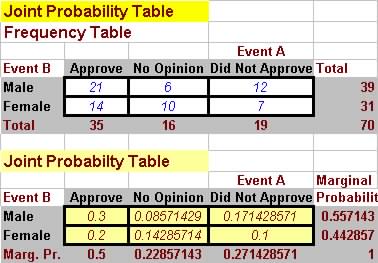
	Approved	No Opinion	Did not approve
Male	21	6	12
Female	14	10	7

If a mathematics major is selected by chance, Find the probability that

(a) The student is a female, given no opinion

(b) The student is a male, given the student does not approve of the change

(c) The student is male and approves of the proposed change. (Multiplication Rule)

Solutions:

Construct a Joint Probability table:

(a) Pr[female|No Opinion] = Pr[female and no opinion] / Pr[no opinion] = 0.1429 / 0.2285 = 0.6254

(b) Pr[male|not approve] = Pr[male and not approve] / Pr[not approve] = 0.1714 / 0.2714 = 0.6315

(c) (Multiplication Rule): Pr[male and approve]=Pr[male] x Pr[approve] = .5571 x .5 = 0.2786
 

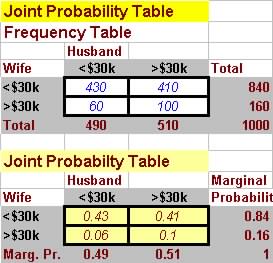
Question 10.  A city has 1000 married couples with both husband and wife working. Each person was asked
whether his or her salary exceeded $30,000. The follow information was obtained:
 

Wife		Husband
		Less than $30,000	More than $30,000
	Less than $30,000	430	410
	More than $30,000	60	100

If one couple is selected at random.

(a) Find the probability that a husband earns less than $30,000, given that the wife earns less than $30,000.

(b) Find the probability that a wife earns more than $30,000, given her husband earns more than $30,000

(c) Are the salaries of husband and wife statistically independent?

Solutions:

Construct a joint probability table:

(a) Pr[Hus <$30k|Wife <$30k] = Pr[Hus and Wife]/Pr[Wife] = 0.43 / 0.84 = 0.5119

(b) Pr[Wife >$30k|Hus >$30k] = Pr[Wife and Hus]/Pr[Hus] = 0.1 / 0.51 = 0.1961

(c) Since you have Pr[Husband and Wife] in all combinations > 0, they are not independent
 

Question 11 Ten people are in a line to purchase tickets. In how many different ways can the 10 people be lined up?

Possible ways would be 10! = 3,628,800

Question 12. The letters A, B, C, D, E, and F are to be randomly arranged in a row. Find the probability that

(a) The arrangement is ABCDEF

(b) The first three letters, in order, are ABC

(c) The letters A and B appear next to each other in either order.

Solutions

(a) The total possible arrangement is n! = 6! = 720 and since ABCDEF is a unique arrangement out of
all the possible 720, the Pr[ABCDEF] = 1/ 720 = 0.00138888. = 0.014

(b) The Pr[1st 3 letters is ABC] means that the remaining 3 letter can be arranged 3! ways = 6

So Pr[1st 3 letters is ABC] = 6 / 720 = 0.0083..

(c) The letters A and B appear next to each other in either order.

So out of the 720 what are the proportion of AB or BA appearing? -

Since there are six places: 1, 2, 3, 4, 5, 6 AB can occupy 2 out of 6 places so Pr[of getting AB or BA] = 2 / 6 = 1/3

Question 13.. - Sample without Replacement - Probability Tree Diagram

Suppose a company's quality assurance department received a shipment of 100 items, 95 are assumed to be good
and 5 bad (the shipment is 5% defective).

Construct a tree diagram (alternate table matrix) that show the probability of selecting a quality control sample of 3 items
without replacement from a population of size 100.

Solution: A Probability Matrix simulating sample selection and their probabilities:

Let D = Defective and G = Good, example G₂ = 2nd sample is Good and D₁ = 1st sample is bad.

Sample without replacement
 

First  Observation	Second Observation	Third  Observation	Sample Space	Probability
5/100 D1	4/99 D2	3/98 D3	D1 D2 D3	0.0000618
		95/98 G3	D1 D2 G3	0.0019584
	95/99 G2	4/98 D3	D1 G2D3	0.0019584
		94/98 G3	D1 G2 G3	0.0460214
95/99 G1	5/99 D2	4/98 D3	G1 D2 D3	0.0019584
		94/98 G3	G1D2 G3	0.0460214
	94/99 G2	4/98 D3	G1G2 D3	0.0460214
		93/98 G3	G1 G2 G3	0.8559988
Eg. Pr[D1 and D2 and D3]=Pr[D1] x Pr[D2|D1] x Pr[D3| D1 and D2] =  =				1