Hypothesis testing is a procedure that examines two alternative positions in which a test is made to determine which of the positions may be true within certain level of confidence.

The position that states that things are the same is called the null hypothesis; the position that states that things are not the same is called the alternate hypothesis. In accepting the alternate hypothesis one rejects the null hypothesis and in accepting the alternate hypothesis, one rejects the null hypothesis.

1. Know the definitions of the two opposing positions for an hypothesis test.

There are two positions or views for an hypothesis test:
 

(1) The null hypothesis is a statement asserting no change or difference about a population parameter; it is denoted by the symbol H0.

(2) The alternate hypothesis is a statement that rejects the null hypothesis or a statement that might be true if the null hypothesis is not; it is denoted by the symbol Ha. The alternate hypothesis may contain the symbol, >, <,

Example: If one wishes to test that the sample mean = the population mean given normal errors of experiments. Then one would, for example, compare the value of the sample mean with that of the population mean and if the difference is small, then one would accept that both are the same or that

The null hypothesis is not rejected (almost saying that its is true) or .

Know how much the difference in comparing both means will be in order to reject the null hypothesis (that both means are not the same) is a matter of probability or how confident or certain you want to be in making that judgment.

In hypothesis testing we present this view of deciding on a level of acceptance of the null hypothesis: If there is a low probability that we can reject the null hypothesis, then we say that the null hypothesis "is true."
 

Note statisticians never say that we accept the null hypothesis, but rather that there is no significant reason to reject it.

This low probability of rejecting the null hypothesis is called the significant level, and is called alpha or denoted by the symbol, a or .

2. Know the meaning of the test statistics used in hypothesis testing.

Acceptance Criterion.

The goal of statistical hypothesis testing for this chapter and many others using a distribution for the test, say a normal distribution is to accept the null hypothesis if the statistical estimator falls within the acceptable blue region of the confidence interval based on the level of significance or probability of acceptance and to reject if its falls in the red region. See Figure 7b.1 below:
 

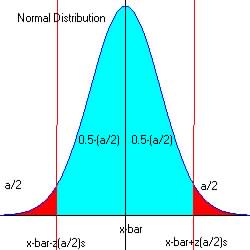The test statistics is the value or quantity that is used to make a decision in testing the hypothesis.

If the blue region is the acceptable region then the red region is the rejectable regions.

For every possible types of statistical tests there are preferred test statistics used to make judgment about the null hypothesis, in the next several chapters we will study many of these.

Example: If the acceptable region for a test is the blue region and its confidence interval is , then a value z = 2.0 falls outside this region so the null hypothesis is rejected; however a value of z = 1.14 falls within this region so there is no reason to reject the null hypothesis.

Throughout this text we will use the phase "there is no reason to reject the null hypothesis" when "accepting" the null hypothesis .

The critical region is the region outside the confidence interval for z that favors the alternate hypothesis - The red region.

The values of z at the endpoints of the critical region is called the critical values. In the last example, the critical values are .

3. Know the meaning of the critical region and level of significance of the hypothesis test.
 

The critical region is the values of the test statistics that provides evidence in favor of the alternate hypothesis. Therefore, a value in the critical region results in a decision to reject the null hypothesis.

Alpha or  is the level of significance of the hypothesis test and it is the probability that the test statistics will fall in the critical region or the red area if the null hypothesis is true.

4. Know the two types of errors associated with hypothesis testing.

Type I error (producer's risk)

Even though it is unlikely that the test statistics will fall into the critical region (red) when the null hypothesis is true, it is still possible.

When this occurs, we reject H₀, when indeed it is true, and therefore make an error in doing so.
 

A Type I error is an error in rejecting the null hypothesis when it is true, and this happens if the test statistics falls inside the critical region (red).

The probability of rejecting the H₀ when it is true is called , where

Type II error (consumers's risk)

Another type or error is to not reject the null hypothesis when it is false. This is called a type II error. It is the probability that not rejecting the null hypothesis when it is indeed false.

This happens when the test statistics does not fall in the critical region when H₀, is false.
 

A Type II error is an error in accepting the null hypothesis when it is false, and this happens if the test statistics falls inside the acceptable region (blue) when it should be fallen in the red region or critical region.

The probability of accepting the H₀ when it is false is called , where

5. Know the basic steps taken to perform a hypothesis test.

These are the steps required to perform a hypothesis test.
 

Summary of Hypothesis Testing: Step 1. Identify the null and alternative hypothesis. The null hypothesis often contain the = sign and  The alternative hypothesis contain >, < and  sign. Example: H0: m1 = m2 and Ha m1 > m2, Step 2. Choose the level of significance of the test, . Since  is the Type I error, the probability of rejecting the null hypothesis when it is true, the smaller the  value the more critical the test. Typical values of  are 0.05, 0.1, 0.001, etc. The probability of acceptance of confidence interval is 1- . Step 3. Select the test statistics This is often based on sampling data or estimates about the population parameters with some standard error of the estimate. This is compared against as expected or reference value often looked up from some probability distribution table. Step 4. Determine the critical region. The critical region is those values of the test statistics that strongly favor the alternate hypothesis. Often its is a good practice to sketch the critical region (red). See Figure above. Step 5. Make your decision. If the test statistics falls into the critical region, reject H0. When this occurs we say that the results are statistically significant.

Worksheet - Hypothesis Testing

Choose Test Name: (e.g. Chi-square Goodness-of-fit):__________________________________________

Enter sample and population parameters:                               Others: Sample size, n = _____ = ________ or  = ____________ = ________ or  = ____________
(1) Select Null Hypothesis: H0		Alternate Hypothesis: Ha
(2) Choose level of Significance, : ________ Write  = ________		Enter degrees of freedom, d.f.
(3) Write and Compute the Test Statistics (e.g. z-score and t):
(4) Select Critical Region of Test Criterion:
Lower-Tailed Test	Two-Tailed Test		Upper-Tailed Test
(5) Make Decision: