The zeros of a function is often referred to as the value of the independent variable(s) when y = 0 or the function is zero. For a quadratic function you can have 3 cases when y = 0. Either the function does not exist for y = 0 or the function have one value for x for y = 0 ( the vertex of the function touches the x-axis or there are 2 values of x when y = 0 (y = a(x - r)(x - s) ).

Table 5.5.6 Zeros of Quadratic Functions (when y = 0)
 

No Figure 5.5.7 zero for function

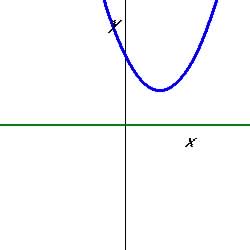
Figure 5.5.8 One zero

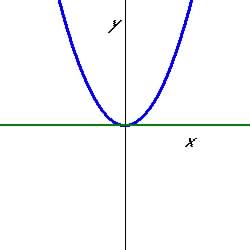
Figure 5.5.9 Two zeros for function

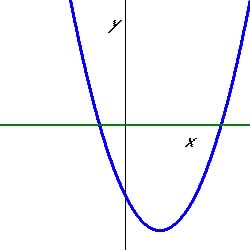
Zeros by Factoring

The zeros of the quadratic function can be easily obtained if one can factor the quadratic function into the Zero Form of the model: y = a(x - r)(x - s) for the zeros are simple x - s = 0 = x - r, where r and s are constants.

Example 5.5.7 Find the zeros of the formula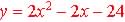 

Table 5.5.7. Zeros of Quadratic by Factoring

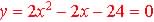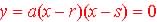
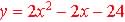
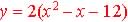
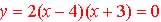
Factor  into the form Factor out 2:  So zeros 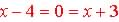 So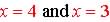

Figure 5.5.10 Zeros by Factoring

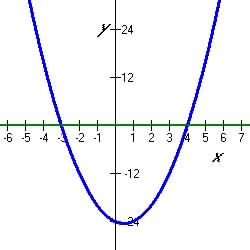
Zeros from the Quadratic Formula:

The zeros of the quadratic function if one exist can be determined given the coefficients of the terms in the Standard Form of the model: 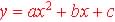 by solving for x in the quadratic formula below:
 

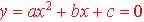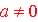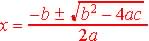
The Quadratic Formula The roots or zeros of the quadratic equation , where , are  When the content of the square root of the quadratic equation, 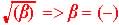 is negative number then the roots or zeros of the function if one exist is not a real number.

Example 5.5.8 Find the zeros of the formula by using the quadratic equation for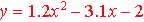 

Table 5.5.8. Zeros of Quadratic by Factoring
 

Find the zeros of 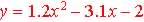 using the Quadratic Equation:

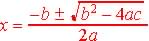
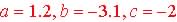
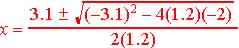
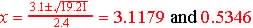
Figure 5.5.11 Zeros from Quadratic Equation

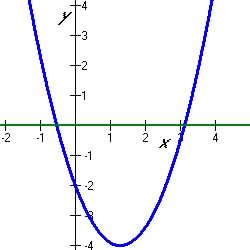
The y-intercept, when x = 0.

The y-intercept of the quadratic and any other function is the value of the function for a single variable, x when x = 0.

The y-intercept for the quadratic function must exist whether it is at the origin at (0, 0) or any other point.

Table 5.5.9. Examples of y-intercepts from Chapter Figures

The table below state the y-intercepts for various Figures Used in this Chapter

Figures	Value of y-intercept - f(x=0)
5.5.1	4
5.5.2	6
5.5.3	-12.5
5.5.4	1
5.5.5	2
5.5.6
5.5.7	(+)
5.5.8	0
5.5.9	(-)
5.5.10	-24
5.5.11	-2

Precalculus: Contemporary Models
by Pin D. Ling