The quadratic model is a very common model used in physical science and mathematics and often is associated with motion or distance and time. If a ball is thrown into the air a quadratic function would best describe the distance of the ball from a fixed horizontal position with respect to time.

The quadratic function is a function of the form: , where a, c, and c are constants.

The height, h(t) of a ball in feet from the top of a tree thrown vertical with respect with time, t in second. may be a quadratic model shown by the formula .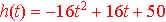

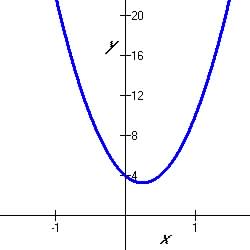
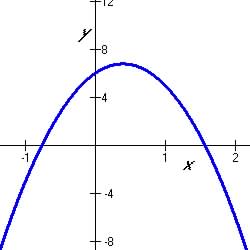
The graphs of quadratic function have symmetrically characteristic shapes that looks like the Figures below:

Table 5.5.1 Optima of Quadratic Functions
 

Figure 5.5.1 Quadratic Maximum

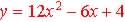
Figure 5.5.2 Quadratic Minimum

A quadratic function is also a polynomial and like polynomials the zeros of the function helps define many characteristics for the model.

There are three forms for the quadratic function that is presented in this text:

1. The Standard form: , where a, b, and c are constants

Example 

2. Vertex Form: 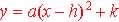, where a is a constant and (h, k) is the coordinate of the vertex

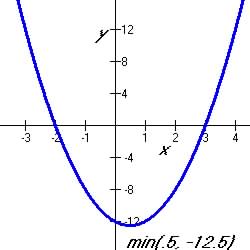
Example 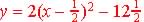, where the vertex or the minimum of the function is at 

( ½ , 12 ½ )

3. The Zero Form: 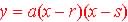, where a, r and s are constants

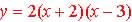Example , and the graphs crosses the x-axis at x = -2 and x = 3

So 

Table 5.5.2 Graphical Representation of Various Quadratic Functions
 

Figure 5.5.3 Quadratic Graphic Equivalency

Precalculus: Contemporary Models
by Pin D. Ling