| Introduction to Linear Models
Linear functions are functions with a constant rate of change or a constant
slope between any interval or 2 points only its curve. The graphs of linear
models are straight lines. Most rates are by definition linear models or
functions: $ pay per hour, miles per gallon,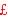 
per $, $ price per gallon, miles per second per second, etc. The general
form of the linear models used is this text is the slope-intercept form
and is:
 ,
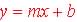where m is the slope of rate of change and b is the y-intercept (the point
where the linear curve crosses the y-axis, or the value of y when the independent
variable, x = 0.
| Linear
Model is a functions characterized by a constant rate of change between
any intervals.
 ,
where m and b are constants, and m is y-intercepts and b is the slope.
Linear Models are straight line curves
Other forms of Linear Model:
Point-Slope Form:  ,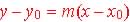
where m is the slope and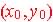 
is a point on line
Standard Form:  ,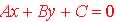
where A, B, and C are constants |
The Graphs below are examples of linear models:
Table 2.1 Graphs of Linear Models:
Most simple relationships like conversion factors are linear models
or directly proportional functions:
12 inches = 1 foot
3 feet = 1 yards
16 oz = 1 pound
Example 1. Write a simple formula that coverts inches to feet:
Feet = F =  ,
where x is in inches, so Formula is  ,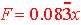
note 0.083 is the slope or rate of change and is a constant value and the
y-intercept is equal to 0.
Caution: When
working with conversions remember to be consistent with the units being
used through your mathematical models. If the rate is feet per second,
then the length should be in feet and the time in hours and if otherwise
convert to consistent units.
Standard for of Linear Models:
The standard for of the linear function is:
 ,
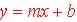So given any two points from a linear model, we can find the equation of
the line that defines it. Often these two points can be obtained from a
paired list of values in a table or two coordinate points from a graph
or two points given or implied from a word problem or enough information
from a formula.
There are other forms of the linear model, but this text will used only
the standard form above for simplification purposes and because this form
is best for working with word problems.
Precalculus: Contemporary Models
by Pin D. Ling |
