|
Investments and The Exponential
Model
Most financial institutions uses the exponential model to apply interest
to funds invested into most of its accounts. Some investment options are
set by the financial institution such as bank interest rate on mortgages
or the interest rates may vary over several terms of the investment or
loan.
These models are mostly exponential growth models (unless an investment
is losing values). They are exponential growth models because growth is
applied per period by a fixed percent.
In most of today's exponential models the percent rate may varies with
time, but in this text we will only concern ourselves with fixed rates
per period.
When an investment, B, follows an exponential growth model
with a fixed rate per period, say a period of one year, the investment
model with respect to time is written as:
Annual Interest Rate:
| Yearly Exponential Growth Model,
i.e. Interest is applied at a fixed percent rate at the end of each year.
 ,
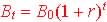where Bt is the balance at time t,
year, B0 is the initial investment amount and r
is the decimal equivalence of the yearly percent rate.
|
Whenever the interest or rate of growth per period is yearly we call
that the annual rate or nominal rate.
Example 4.9 Find the balance in a checking account after 5 year,
if $2,000 was originally deposited into the account yielding an annual
interest rate of 3.5%.
This is an exponential growth model with an periodic or yearly interest
rate of 3.5% or r = 0.035.
So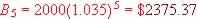 
, the balance in the checking account after t=5 years.
This process of apply an interest to the balance of an account or fund
per defined period is called compounding. For year interest rate increases
we have a yearly compounding.
Compounding Greater
than Yearly
| If n is defined as
the number of period in a year, then we define periodic compounding
as:
 ,
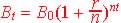where Bt is the balance at time t,
year, B0 is the initial investment amount and r
is the decimal equivalence of the yearly percent rate.
Example compounding is monthly, n = 12; quarterly, n =
4, daily, n = 365 |
Continuous Compounding
When the number of compounding per
yearly is large, even greater than hourly where,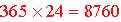 
we defined this as continuous compounding:
 ,
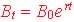where Bt is the balance at time t,
year, B0 is the initial investment amount and
r is the decimal equivalence of the yearly percent rate.
|
With all these various types of compounding one often need to evaluate
each compounding as its compares to the yearly compounded interest rate,
we call this normalization the Effective
Annual Rate.
The Effective Annual Rate is found by setting the various compounding
equal to each other and finding the equivalence to the yearly rate of r',
from (1+r').
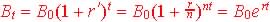
Or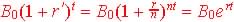 
Divide by B0 we get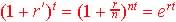 
Or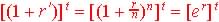 
Or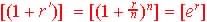 
So the effective annual rate for periodic compounding is the solution
of r' from
 ,
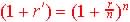where r is the annual rate and r' the Effective
Annual Rate.
And the effective annual rate for continuous compounding is the solution
of r' from
 ,
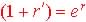where r is the annual rate and r' the Effective
Annual Rate.
Example 4.10 Find the possible balance(s) of a college fund with
an initial investment of $50,000 after 25 years if it allowed to grow at
an annual interest rate of 5.25% in the following portfolio or accounts:
Compounded Yearly, Monthly, Daily and Continuously. For each portfolio
find the effective annual rate.
Table 4.6 Investment Alternatives in Exponential Growth Funds:
| Compound Period |
Formula / Calculation
For Balance
 ,
|
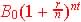Balance
after 25 years
where  |
Calculation
for Effective Annual Rate
(1+r'), where r' is the Effective Annual Rate |
Effective
Annual Rate, % |
| Yearly, n=1 |
 |
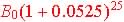$179,689.47 |
 |
5.25% |
| Monthly, n=12 |
 |
$185,241.48 |
|
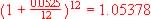
5.378% |
| Daily, n = 365 |
 |
$185,755.00 |
 |
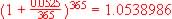5.3899% |
| Continuously n is large |
 |
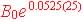$185,772.54 |
 |
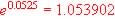5.39% |
Precalculus: Contemporary Models
by Pin D. Ling
|
