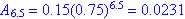Tell whether the relationships of N and M shown in the table below is a function or not. If it is a function which variable is the input and which is the output variable and why? (Give reasons for both answers)
| N | 1 | 0 | 1 | 0 | 8 |
| M | -3 | 2 | -3 | 2 | 1 |
Both N and M can be functions since there are only one value for the output variable when the input variables are the same, e.g. N(0) = 2 and N(1) = -3 also M(2) = 0 and M(-3) = 1.
Question 2 - Find the slope of the
function  between between
(a) x = -2 and -1 and (b) x =1 and x = 2
Note the shape of the function between both domains. |


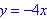
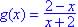
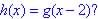 (b) What is h(1)?
(b) What is h(1)? 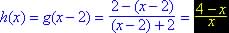
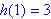
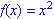 and
and 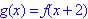 what is
what is 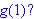
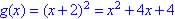
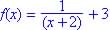 ?
?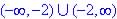
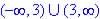
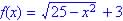 ?
?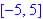 (sqrt cannot contain a real negative number)
(sqrt cannot contain a real negative number)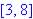 (smallest y is when sqrt = 0, 3 and largest
y is when x = 0 or y = 5 + 3 = 8)
(smallest y is when sqrt = 0, 3 and largest
y is when x = 0 or y = 5 + 3 = 8)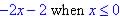 and
and 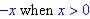
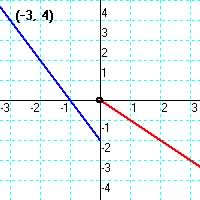
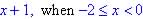
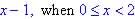
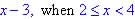 -
Function is undefined for x when f(x) =1 (will give partial credits
if skecth graph)
-
Function is undefined for x when f(x) =1 (will give partial credits
if skecth graph)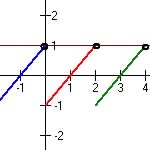
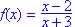 .
.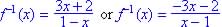
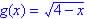
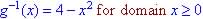
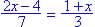
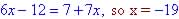
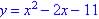
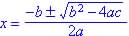
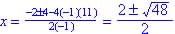
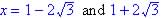
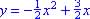 ; if none
exist state why.
; if none
exist state why.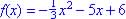 ?
?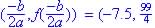 )
)