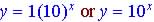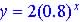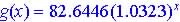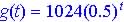Lesson 9 - 3.2#1 Explain difference between Linear and Exponential growth: Linear growth occurs at a constant positive amount each period while exponential growth occurs at a constant percent increase each period.	Lesson 9 - 3.2#3 - Comparing Exponential and Linear Decreasing Functions: (a) P = -100t + 5000, linear function since decreases at a constant amount of 100 each year from 5000. (b) P = 5000(0.92)t , exponential since decreasing at a rate of 8% or r = 0.08 year from 5000.
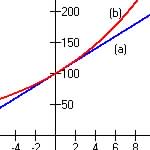
Lesson 9 - 3.2#2 - Comparing Exponential and Linear Increasing Functions: (a) P = 10t + 100, linear function since increasing at a constant amount of 10 each year from 100. (b) P = 100(1.10)t, exponential function since increasing at a constant percent rate of 10% each year from 100. (c) Graph of both functions	Lesson 9 - 3.2#10 - Determining whether a function is linear or exponential from table of values. If linear constant amount change 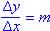and if exponential constant ratio change 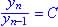. f(x) increases at a constant amount, 0.87965 each change is x, so f(x) is linear. g(x) change by a constant ratio each successive g(x), e.g. 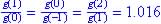, so g(x) is exponential. h(x) is neither linear nor exponential since above rule does not apply.
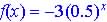
Lesson 9 - 3.2 #12 Find formula for exponential with points f(-2) = -12 and f(3) = -3/8. Ans. :	Lesson 9 - 3.2 # 15 Find formula of exponential increasing graph with points: (0, 1) and (2, 100) Ans. :

Lesson 9 - 3.2 #20 Find exponential decreasing function from decreasing function graph with points (-1, 2.5) and (1, 1.6) Ans.:	Lesson 9 - 3.2 #23 Find formula from a table of values: Exponential Increasing Functions so: Using points (6, 100)) and (9, 110) Ans.:
Lesson 9 - 3.2 #24 Find formula from table of values: Neither linear nor exponential (state why) So no formula that we know of yet.	Lesson 9 - 3.2 #25 Find formulas from table of values: Exponential decreasing function: Using points (1, 512) and (2, 256) Ans.: