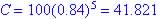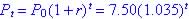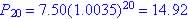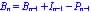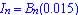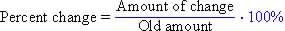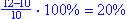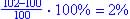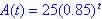Lesson 8 - 3.1#1 Finding an exponential formula given initial value of 70 millions and growth rate 1.9% per year: At end of 1st year: 100% + 1.9% = 101.9% P = 70(1.019) At end of 2nd year: P(1.019)(1.019) = 70(1.019)2 At end of 3rd year: P(1.019)(1.019)(1.019) = 70(1.019)3 At end of t-th year: P = 70(1.019)t

Lesson 8 - 3.1#5 Find growth factor of an exponential increasing functions: Given: growth at rate of 28% per decade Then r = 0.28 Growth factor is the (1 + r) = 1 + 0.28 = 1.28

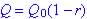
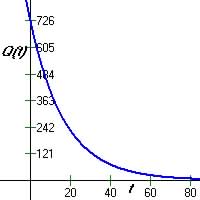
Lesson 8 - 3.1#3 Finding an exponential formula for a decreasing (decay) function given initial value of 726 grams and decaying at a rate of 5.626% per year: The rate of decay is 5.626% / year so growth factor is 1 - 0.05626 = 0.94374 Since exponential decreasing functions, a general formula is (a) So formula is 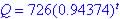(b) A graph of the function is

Lesson 8 - 3.1#13 Given a problem with percent rates change over time find outcome. Given: 500 items, increase by 42% then decrease by 42%. Ans.: 411.8 Since 42% increase yields: 500 (1.42) = 710 And 42% decrease yields: 710(1 - 0.42) = 710(0.58) = 411.8 Lesson 8 - 3.1#19 Study of exponential decreasing function (caffeine elimination at 16% per hour). (a) Since C0 = 100 mg, Ct = 100(1-0.16)t (b) If C is amount of caffeine in body each hour after consumption, then C = 41.821 mg when t = 5 hours. Since

Lesson 8 - 3.1#20 Rate of inflation (3.5%) problem. Price of movie tickets. Given: Initial price is $7.50 and rate of inflation is 3.5%. (a) Formula of exponential increasing function is (b) In 20 years, movie tickets will cost $14.92 Since

Lesson 8 - 3.1#23 The Credit card problems (Exponential increasing a decreasing functions) Given: Interest is 1.5% monthly on balance Minimum Monthly payment is 2.5% of balance. (a) table of monthly balance Month Balance, B Interest, I Min Payment 0 $2,000.00 $30.00 $50.00 1 $1,980.00 $29.70 $49.50 2 $1,960.20 $29.40 $49.01 3 $1,940.59 $29.11 $48.51 4 $1,921.19 $28.82 $48.03 5 $1,901.98 $28.53 $47.55 6 $1,882.96 $28.24 $47.07 7 $1,864.13 $27.96 $46.60 8 $1,845.49 $27.68 $46.14 9 $1,827.03 $27.41 $45.68 10 $1,808.76 $27.13 $45.22 11 $1,790.67 $26.86 $44.77 12 $1,772.76     Total   $340.84 $568.08 (b) After one year your unpaid balance is $1772.76. You have paid off $2000 - $1772.76 = $227.24 and the interest you have paid is the sum of the middle column, $340.84.

Lesson 8 - 3.1#24 Calculating percent changes. (a) What is percent change from 10 to 12? (a) So 10 to 12 is (b) So 100 to 102 is

Lesson 8 - 3.1#25 Study in Exponential Model. Given the amount of drug (mg) in the body after t hours from consumption is (a) The initial dosage is A0 = 25 mg (b) Since 0.85 = 1 - r, the rate of drug leaving the body is r = 0.15 or 15%. (c) A10 = 25(0.85)10 = 4.922 mg (d) t = 20 hours (by trial and error, substitute values of t and stop when A(t) < 1.)