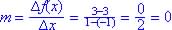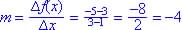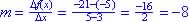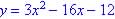
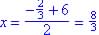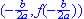
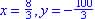
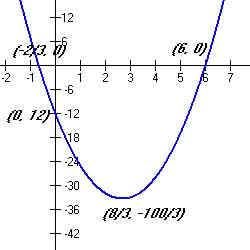
Lesson 8 - 2.6#11 Sketch the graph of a quadratic function from its formula using info about is vertex and intercepts. Zeros are since by factoring (3x+2)((x-6)=0 The vertex is midpoint (axis of symmetry) or So vertex is So Zeros 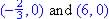; y-intercept at 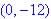and vertex (minimum since a is positive) at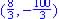	Lesson 8 - 2.6#12 Study of the concavity of a quadratic function based a study of its rate of change. x f(x) Rate of change -1 3   1 3 Between x = -1 and x = 1 3 -5 Between x = 1 and x = 3 5 -21 Between x = 3 and x = 5 Since the rate is decreasing the functions is concave down.
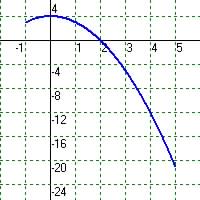
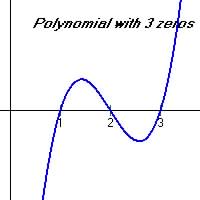
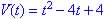
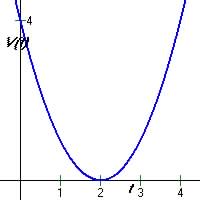
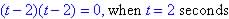
Lesson 8 - 2.6#12 Study of polynomials and quadratic. Ans.: No the graph with 3 zeros cannot be a quadratic function, since a quadratic function can only have at most 2 zeros (or points where the graph crosses the x-axis)	Lesson 8 - 2.6#16 Study of velocity (quadratic function) (a) V0 = 4, Since initial velocity is V(t) when t = 0 (b) Object is not moving when V(t) = 0 or (c) The graph is concave up (a quadratic function with a minimum)

Notes of Problems 2.6# 12 and 2.6#16

2.6#12 - A polynomial with zeros at x = 1 , x = 2 and x = 3 should look live this (many possibilities)

Graph of 2.6#16 is concave up