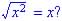
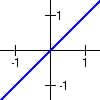
(a) Graph of both functions: (not the same)
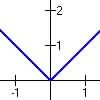
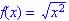 (abs value) (abs value)
|
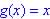
|
(b) Comparing table of values 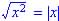
 |
-5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
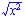 |
5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 4 | 5 |
(c) 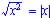 because graphs overlap and they share the same
piecewise functions:
because graphs overlap and they share the same
piecewise functions:
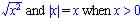
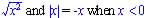
(d) Graphing 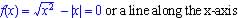
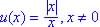
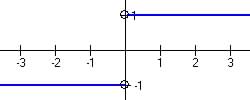
(a) Graph the function (undefined at x = 0)
 |
(b) Table agrees with observations in graph
 |
-5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
 |
-1 | -1 | -1 | -1 | -1 | U | 1 | 1 | 1 | 1 | 1 |
(c) Domain is all x except x = 0.
The range is -1 and 1
(d) the claim that u(x) = 0 when x = 0 is false since the function is undefined at x = 0.
(a) 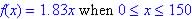
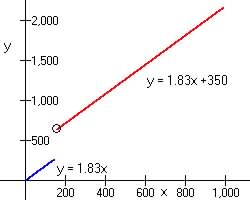
(minimum area is 0 and maximum is given has 150)
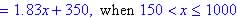
(cost change to new formula after 150 sq. ft
and maximum area given has 1000)
(b) Graph and Domain and Range
|
Domain is Range is and
|
(a) The smallest difference, the smaller the refund:
Is $0.01 (not 0.0) refund is $1.00 + $0.01 = $1.01
(b) Piecewise function is:
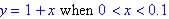 (1)
(1)
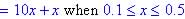 (2)
(2)
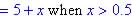 (3)
(3)
(c) Find x when y = $9.00 - Only equation (3) can give a refund value high enough, so solve:
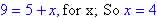
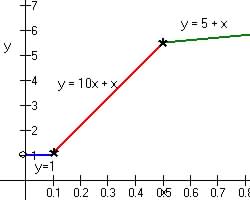
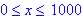
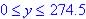 ( for 1st
domain)
( for 1st
domain)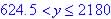 (fro 2nd
domain)
(fro 2nd
domain)