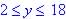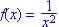 given the domain
given the domain 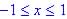
Ans.: Range is 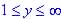
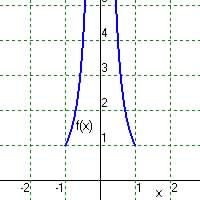
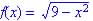 given the domain
given the domain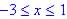
Ans.: Range is 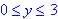
 .
.
Ans.: Denominator cannot be zero
Domain: 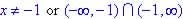 Range:
Range: 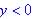
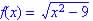 .
.
Ans.: Cannot have sort of negatives
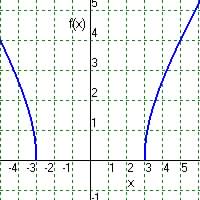
Domain: x2 -
9 >= 0, so 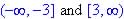
Range: for
x above 
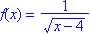 .
.
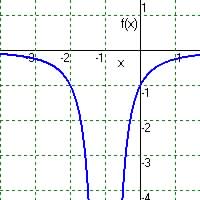
Ans.: cannot have sort(-) and demon. cannot be zero
Domain: x -
4 > 0, so 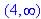
Range: since x is above, y > 0
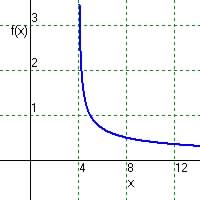
 .
.
Ans.: Can have cube roots of any negative and positive numbers
Domain: is all values of x
or 
Range given x above is all values of y
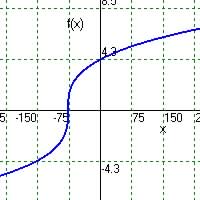
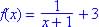 .
.
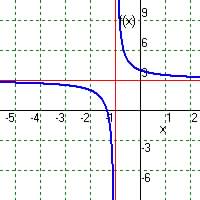
Ans.: demon. Cannot be zero
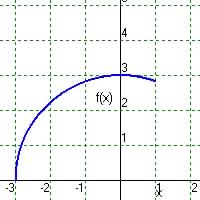
Domain: x cannot
be -1 or 
Range: Since
given x above 1 st term never = 0, so y never quite equal 3 so 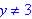
 .
.
(a) p(0) = 50, p(10) = 131,
p(50) = 911
(b) Graph between 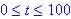
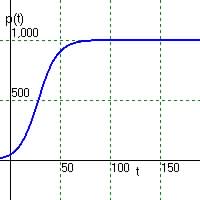
(c) Range is 50 to 1000, since t = 0 give p = 50 and t = 100 give p equal to about 1000
The rabbit population reaches a maximum about t = 100.
(d) Smallest p is when t = 0 at p = 50 and as t gets large (0.9)t => 0 so demon. = 1+0 and so p would have its largest value at 1000
Domain is 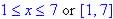
Range is