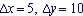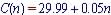
Section 1.3 #2 Determine if a table of values represents a linear function. The function is a linear function since for every (constant rate throughout the function)	Section 1.3 # 7 Identify y-intercept and slope fro a linear formula, y-intercept is $29.99 and slope, m is 0.05 (cost per minutes)
Section 1.3 #12 Find formula from linear problem statement. Given population in 2002 is 18,310 (P0) and growth rate per year (t) is 58 people. Formula is P = 18310 + 58t.	Section 1.3 #13 Properties of Linear Function from table of values. (a) Table is linear function since constant rate: 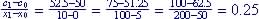(b) Linear plot with points (0, 50) & (100, 75) (c) Slope is 0.25 (a) and (d) When x = 0, C = $50, setup cost
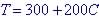
Section 1.3 #18 Linear Depreciation Formula Given: Cost from new Car is $21,000 and depreciates by $10,500 in 3 years. So yearly depreciation is 10500/3 = $3500 Depreciation means negative rate, so m = -$3,500. Formula for depreciation since new is V(t) = 21000 - 3500t	Section 1.3 #20 Interpreting linear tuition cost, T with respect to number of credits for part-time students. (a) T when C = 8 is T = 300 + 200(8) = $1900 (b) C when T = 1700 is 1700 = 300 + 200C C = (1700 - 300) / 200 = 7 (c) Table of values for C = 1 to 12 credits C 0 2 .. 10 11 12 T 500 700   2,300 2,500 2,700 T/C 500 350   230 227 225 (d) The lowest cost per credits is when C = 12 of 225 (e) The cost of 300 represents fixed cost like registration cost (f) The 200 represents the rate or cost for each additional credits