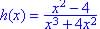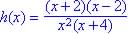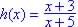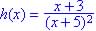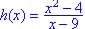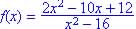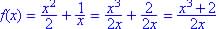
Lesson 27 - 9.4 #1 Write as a rational function in for r(x) = p(x) / q(x).	Lesson 27 - 9.4 #2 Write as a rational function in for r(x) = p(x) / q(x). This is not a rational function since 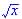is not a polynomial.
Lesson 27 - 9.4 #7 Discuss long term behavior of rational functions:.	Lesson 27 - 9.4 #10 Determine the horizontal asymptote for .
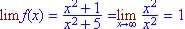
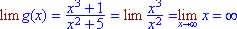
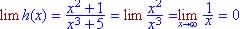
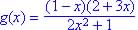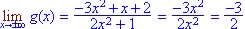
Lesson 27 - 9.4 #11 Determine the horizontal asymptote for Lesson 27 - 9.4 #17 Study of rational function (average cost): (a) 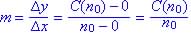(b) a(n0) = C(no)/no, slope is same as average cost.	Lesson 27 - 9.4 #16 Study of asymptote for C(n) = 500 + 50n and a(n) = C(n) / n (a) (i) C(1) = $5000 for 1 unit (ii) C(100) = $10,000 for 100 units etc (b) (i) a(1) = C(1)/1 = $5050 / unit to make 1 unit (ii) a(100) = C(100)/100 = $100/unit to make 100 units etc. (c) As number of units increases ave cost per unit gets closer to $50/unit.
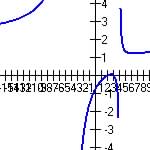
Lesson 27 - 9.4 #19 Study of average cost. (a) C(x)= 3000 + 3x (b) a(x) = C(x) / x = (30000 + 3x) / x = 3 + 30000/x (c) Graph is shown like 1/x with HA = 3	9.4 #19 cont. (d) Cost $3 to produce (e) as x gets close to 0, average cost gets large. (f) x = 30000 / (y - 3)

Pg. 406: 3,5,6,8,10,19

Lesson 27 - 9.5 #3 Find asymptotes, interecepts for No y-intercept, x-interecepts: (-2, 0) and (2, 0), HA = 0 and VA at x = 0 and -4	Lesson 27 - 9.5 #5 Find asymptotes, interecepts for HA is y = 1, VA is x = -5, y-interecpt at x = 3/5 and x-interecpt at x = -3
Lesson 27 - 9.5 #6 Find asymptotes, interecepts for HA is y = 0, VA is x = -5 , y-int is 3/25 and zero is x = -3	Lesson 27 - 9.5 #8 Find asymptotes, interecepts for No HA and VA at x = 9, y-int 4/9 and zeroes at x = -2 and 2.
Lesson 27 - 9.5 #10 Graph rational function without a calculator HA is y = 2, VA at x = -4 and 4, y-int (0, - ¾ ) and zeros ar x = 2 and 3.	Lesson 27 - 9.5 #19 - Study of transformation of f(x) and 1/f(x). See class lecture