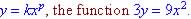
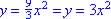
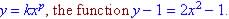
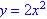
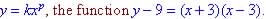
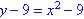
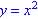
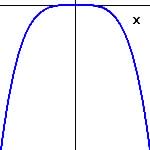
Function is Even (symmetrical about y-axis)
Function is Fractional (steeper near origin and flatter away from it)
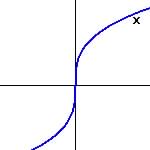
Function is Odd (symmetrical about origin)
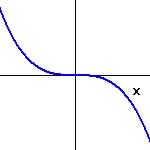
Lesson
25 - 9.1 # 2 Write in form 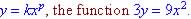
|
Lesson
25 - 9.1 # 3 Write in form 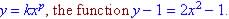
|
Lesson 25
- 9.1 # 6 Write in form 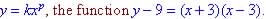
|
Lesson 25
- 9.1 # 7 Determine if graph of power function is Even, Odd
or fractional powers.
Function is Even (symmetrical about y-axis)
|
| Lesson 25 - 9.1 # 9 Determine if graph
of power function is Even, Odd or fractional powers.
Function is Fractional (steeper near origin and flatter away from it)
|
Lesson 25
- 9.1 # 10 Determine if graph of power function is Even, Odd
or fractional powers.
Function is Odd (symmetrical about origin)
|
| Lesson
25 - 9.1 # 13 Find a power function given 2 points: (6, 17)
and (1, 2).
Using the form: (1, y1 ) and (x2 , y2 )
For (1, 2): Using (6, 17) and k = 2:
So power function is |
Lesson
25 - 9.1 # 15 Find formula for inverse proportional
function with points (4, 6).
(a) Formula: Using (4, 6), k is:
So formula is
(b) Find x when y = 8:
|
| Lesson 25
- 9.1 # 30 30 minutes Super Bowl commercial spot in 2002.
Given: (2002, cost = $2 mils for 30 sec) and (1967, cost = same for 22.989 min). (a) Cost in dollars/sec in 2002 is: Cost in dollars/sec in 1967 is: (b) So 2002 cost is Or 46 times more expensive than in 1967 |
Lesson 25
- 9.1 # 37 Expanding oil spill in circular form problem -
200 m per hour:
(a) Express radius of spill as power function. Per hour (b) Express area of spill as power function
(c) when t = 7, Area is:
|
Lesson 25
- 9.1 # 37 Kepler's Law 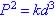 . .
(a) So When P = 365 and d = 93,000,000
(b) For Jupiter, d = 483,000,000, so
|