Given 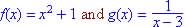
Find 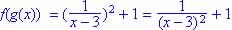
So 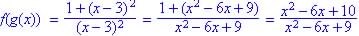
Given 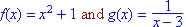
Find 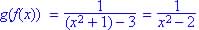
Given graph below:
|
|
(a) f(f(1)) = f(2) = 4
(b) g(g(1)) = g(3) = 1
(c) f(g(2)) = f(2) = 4
(d) g(f(2)) = g(4) = 0 |
Given 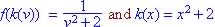
Find 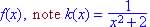
So 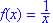
| Lesson
24 - 8.1 #5 Composition from formula:
Given Find So |
Lesson
24 - 8.1 #6 Composition from formula:
Given
Find |
||
| Lesson 24
- 8.1 #29 Composition from formula:
Given graph below:
|
Lesson 24
- 8.1 #51 Composition from formula:
Given Find So |
Pg. 359: 33,37,43 and
| Lesson
24 - 8.2 #33 Solve by using the inverse function:
Solve
|
Lesson
24 - 8.2 #37 Inverse Function -
The function y = sin t fails
the horizontal line test except on certain intervals, here is an
example of one:
|
|||
| Lesson
24 - 8.2 #43 Study of the Area of a circle and its
inverse function -
(a) Area:
(e) Domain A(r) is r > = 0 and Range is A >= 0 Domain of Inverse, r(A) is same as Range of A(r), r > = 0 etc. So inverse only with restricted domain and range. |
||||
Pg. 367: 2,6,7,12,21,31 - Composition of Functions
| Lesson
24 - 8.3 #2 Composition of Function:
Given
|
Lesson
24 - 8.3 #6 Composition of function:
Given Find
|
| Lesson 24
- 8.3 #7 Composition of Function:
Given: (a) (b) (c) (d) |
Lesson 24
- 8.3 #12 Composition of Function:
Given: (a)
(b)
(c)
(d) |
| Lesson 24
- 8.3 #21 Composition of Function:
Revenue = # customers times price per customer R(i) = n(i) x p(i) = (50000 - 2500i)(15 + i)
Max. profit occurs when i = 2.5 (quadratic solution to R(i), vertex (h, k) where h = 2.5) Max. price = 15 + I = $17.50
|
Lesson 24
- 8.3 #31 Composition of Function from word problem:
(a) pop size = sun of men and women
(b) tot money = amt. women make times number of women
|