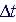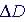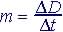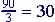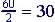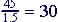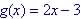
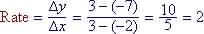
Section 1.2 # 3 - Rate from Direct Proportional Graph of D(miles) as Function of t(hours). (a) (b) Interval   (i)t=2 and t = 5 5 - 2 = 3 150 - 60 = 90   (ii) t=0.5 and t=2.5 2.5 - 0.5 =2 75 - 15 = 60   (iii) t=1.5 and t=3 3 - 1.5 = 1.5 90 - 45 = 45   The average speed is 30 mph (for entire trip)	Section 1.2 # 8 - Rate from formula (a) Rate between (-2, -7) and (3, 3) is (b) The function is increasing over the interval since the average rate of change is positive (c) The function is increasing everywhere.
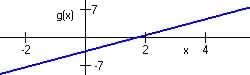
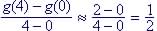
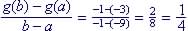
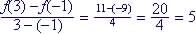
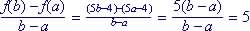
Section 1.2 #10 - Rate of Change from Graph (a) Estimated rate is (b) Line segment for (a) have points: (0, 0) and (4, 2) (c) Estimated rate is since g(-9) is about -3 and g(-1) is about -1 (d) Line segment for (a) have points: (-1,-1) and (-9, -3)	Section 1.3 #11 Rate from Function f(x) = 5x - 4 (i) Between (-1, f(-1)) and (3, f(3)): (ii) Between (a, f(a)) and (b, f(b)): (iii) Between (x, f(x)) and (x+h, f(x+h)):
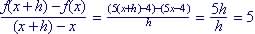
Section 1.2 #14 Interpreting Properties of Function from Graph - sunspots, s with time in years. (shaky periodic) (a) s is a function of t (pass vertical line test) (b) Function increasing on intervals:	Section 1.2 #16 Calculate rate given time and distance intervals: (a) Table 1.2.16 Carl Lewis' Times at 10 m intervals Time (sec) Distance (meters) Rate (meters / sec) 0 - 1.94 0 - 10 1.94/10 = 5.15 1.94 - 2.96 10 - 20 9.8 2.96 - 3.91 20 - 30 10.53 3.91 - 4.78 30 - 40 11.49 4.78 - 5.64 40 - 50 11.63 5.64 - 6.50 50 - 60 11.63 6.50 - 7.36 60 - 70 11.63 7.36 - 8.22 70 - 80 11.63 8.22 - 9.07 80 - 90 11.76 9.07 - 9.93 90 - 100 11.63 (b) He attained his maximum speed of 11.76 meters/sec between 80 and 90 meters. He does not run his faster when he crossed the finish line since speed 11.63 is less than his faster speed.