Pg. 188: 5,6,12,13,16, 17, 31,32,39
| Lesson
14 - 5.1 # 5 - Write and graph transformation of m(n) = ½ n2.
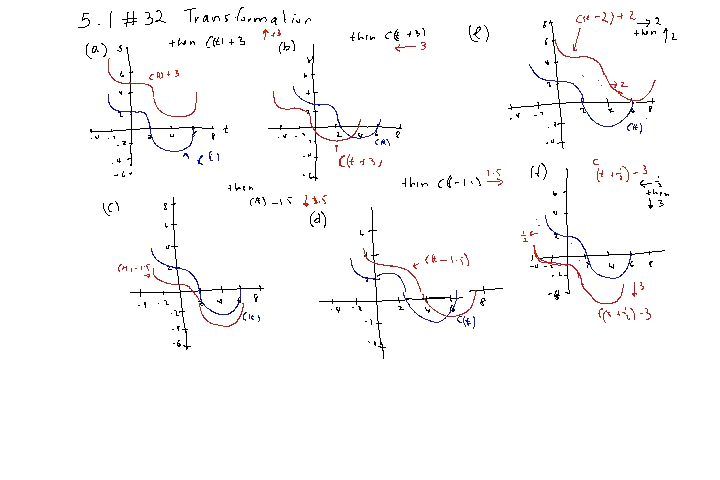
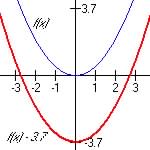
For y = m(n) - 3.7 (Vertical Shift Down)
|
Lesson
14 - 5.1 # 6 - Write and graph transformation of m(n) = ½ n2.
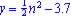
For y = m(n - 3.7) (Horizontal Shift Right)
|
| Lesson 14
- 5.1 # 12 - Write and graph transformation of k(w) = 3w.
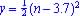
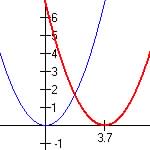
For y = k(w - 3) (Horizontal Shift Right)
|
Lesson 14
- 5.1 # 13 - Write and graph transformation of k(w) = 3w.
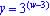
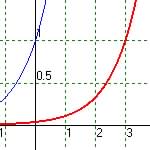
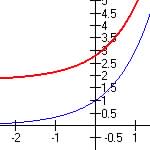
For y = k(w)+1.8 (Vertical Shift Up)
|
| Lesson 14
- 5.1 # 16 - Write and graph transformation of k(w) = 3w.
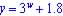
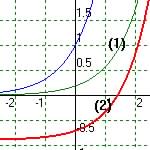
For y = k(w - 1.5) - 0.9 (Horizontal Shift Right then Vertical Shift Down)
|
Lesson 14
- 5.1 # 17 - Match the graphs of the transformation of y
=|x|.
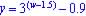
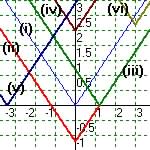
(i) y = |x| (ii) y = |x| - 1.2 (iii) y = |x - 1.2| (iv) y = |x| + 2.5 (v) y = |x + 3.4| (vi) y = |x - 3| + 2.7
|
| Lesson
14 - 5.1 # 31- If S(d) is height of tide on day d of the
year.
(a) T(d) = S(d) + 1 (Height in Tacoma is 1 ft higher than Seattle's height) (b) P(d) = S(d - 1) (Height in Portland is same as previous day's height in Seattle) |
Lesson 14 - 5.1 # 32- Sketch
Transformation - See Solutions (mimio software needed):
Click to see larger image  |
| Lesson 14
- 5.1 # 39- Transformation of a linear function (cost of
evening = cover change plus 3 per drink)
(a) Formula is t(x) = 3x + 5 (b) Price of cover charge is raised by $1 Then n(x) = t(x) + 1 = 3x + 6 (c) Cover charge increase to 410 and first 2 drink free. So p(x) = t(x - 2) + 5 for x > 2 and p(x) = t(x) + 5 for x =< 2 |
