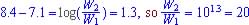Lesson 13 - 4.3 # 2 - Match Graphs of exponential and logs with formulas: Graph A is y = 3x and Graph B is y = 2x since the growth factor b is larger in y = 3x than y = 2x and Graph E is y = e-x since the continuous rate, k is negative. Graph D is y = log x and Graph C is y = ln x , since ln grows faster than log.	Lesson 13 - 4.3 # 3 - Equation of asymptotes: For y = 10x , asym is y = 0 (horizontal) For y = 2x , asym is y = 0 (horizontal) For y = log x, asym is x = 0 (vertical)
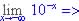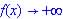
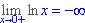
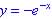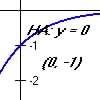
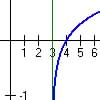
Lesson 13 - 4.3 # 6 - Find value of function at its limits: (look at graphs of functions for clues) (a) as x gets negative large function becomes 10x so function becomes large Positively, i.e. (b)	Lesson 13 - 4.3 # 8 - Find all asymptotes and intercepts for . Functions looks like: The y-int is (0, -1) Horizontal Asymptote at y = 0
Lesson 13 - 4.3 # 26 - Find Domain of function h(x) = ln(x2). Note that for log(x), x > 0 So x > 0 is true when x is both positive and negative for x2 Domain:	Lesson 13 - 4.3 # 29 - Find Domain of function k(x) = ln(x - 3). Note that for log(x), x > 0 So x > 0 is true when (x - 3) > 0 or x > 3 Domain:

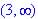
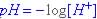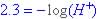
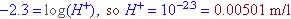
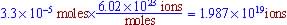
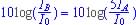
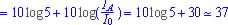
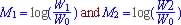
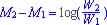Lesson 13 - 4.3 # 32 - Find information of log - exp. Relationships (pH concentration). Note: , where H+ is moles per liter (a) Given pH = 2.3 find H+, (b) Find number of H+ ions in 2 oz of lemon juice: Since 1 liter = 30.3 oz, then 2 oz = 0.066 l. And since there are 0.005 mole H+ icon sin a liter, there are 0.066 x 0.005 = 3.3 x 10-5 moles H+ icons present There are 6.02 x 10 ions in one moles so Number of ions are

Lesson 13 - 4.3 # 33 - Find information of log - exp. Relationships (sound intensity rating) Let IA and IB be intensity of sound A and sound B respectively. Since IB = 5IA and by definition the decibel rating is 10log(IA/I0) = 30 Decibel rating of B = Sound B is 5 times louder than sound A but decibel rating goes from 30 to 37.

Lesson 13 - 4.3 # 35 - Find information of log - exp. Relationships (seismic waves) (a) We know (log A - Log B = Log (A/B) (b) Let M2 = 8.4 and M1 = 7.1, then W2 / W1 is So seismic waves of 1906 earthquake were 20 times as large as those of 1989.