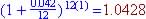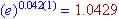Exponential growth: y = a(b)t , where b > 1
Note: the larger the value of b the faster the function grows: So 3 > e > 2

For exponential with continuous percent rate (e) for the form: y = a(e)t , where e = 2.7142.., and k any real number except 0, larger values of k makes the function grows faster.
So fastest percent rate for k is
(a) Graph III
(b) Graph II
(c) Graph IV
(d) Graph I
Exponential increasing function:
Pt = P0(e)kt
(a) Formula is Pt = 25000(e)0.075 t
(b) Yearly rate is r, so find r when
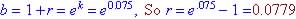
Or rate is 7.79%, Yearly rate must be more to catch up to a continuos rate that grows faster each year.
Rate = 1%, 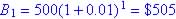
Compounded weekly (n = 52) yields $505.03
Compounded every minutes (n = 52600) yields $ 505.03
Compounded continuously (e) yields $ 505.03
Lesson 10 - 3.4#10 Given nominal rate (yearly interest rate) find balance after t = 1.
Rate = 8%, 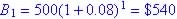
effective annual rate => (1 + (0.01/52)^52 = 1.0100491
or r = 0.0100491
So effective rate is 1.0049%

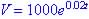 .
.
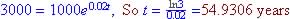
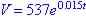 .
.
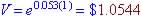
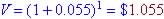 (so
Investment 2 is better - greatest
effective annual rate)
(so
Investment 2 is better - greatest
effective annual rate)