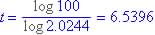Pg. 122: 15,17,31 and Pg. 130: 1,2,3,7,10,14,15,17,19,26

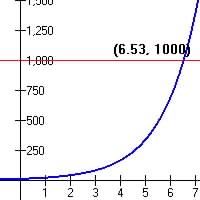
Lesson 10 - 3.3#15 Graphs of Exponential - Study of the City of Boston's Population since 2000: Given: P0 = 651, 000 and declines at a rate of 1.2% per year. Exponential decreasing function: Pt = P0(1 - r)t (a) Formula is Pt = 651(0.988)t (in thousands) (b) Pop in 2010: t = 10 is P10 = 651000(0.988)10 = 576,966 (c) When is pop = 550,000? t = 13.96 years Since	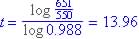Lesson 10 - 3.3#17 Graphs of Exponential - Number of disease cases decreasing at a rate of 10% per year.. Exponential decreasing function: y = y0(1 - r)t (a) Formula is y = 10000(0.90)t , Since y0 = 10000. (b) 5 years from now, y(5) = 10000(0.9)5 = 5905 cases (c) Find t when y(t) = 1000. 1000 = 10000(0.90)t ., t = 21.854 years Since
Lesson 10 - 3.3#31 Graphs of Exponential - Rabbit population growth from 10 to 340 in 5 years. Exponential increasing fct: Pt = P0(1 + r)t (a) Since 340 = 10(b)5, 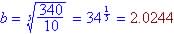Pt = 10(2.0244)t (b) Graphically estimate of when P = 1000 is shown in Figure 10.1 From graph, t = 6.5296 years Since	Figure 10.1 - Find t, when population equals 1000.