Chapter 42 - Examples of Problem in Homework 4 and Workshop Examples
Exponential  Functions

Example 1 - Write a possible formula for an exponential function with an orginal value of 150 and:

(a) Grows at a rate of 0.15 % each day.

(b) Decreases by ¼ its value every hour

Solutions: (a) This is an exponential increasing function of the form: P=P0(1 + r)t, where t is time in days,
r = 0.15 / 100 = 0.0015 (the decimal equivalent of the percent rate, so 1 + r = 1.0015) and
P0 = 150 (the value of P when t = 0).

So possible formula is P=150(1+0.0015)t = 150(1.0015)t: P=150(1.0015)t

(b) This is an exponential decreasing function of the form:P=P0(1 - r)t ,
where t is time in days, r = ¼ converted to its decimal decimal equivalent of 0.25, so 1 - r = 0.75)
and P0 = 150 (the value of P when t = 0).

So possible formula is P=150(1-0.75)t = 150(0.75)t: P=150(0.75)t

Example 2 - (a) Convert P=15(0.75)t to its equivalent P=P0 ekt

Note: P0 = 15 and k = ln(1-r) = ln (0.75) = -0.2877, so formula needed is P=15 e-0.2877t

(b) Convert P=1.25 e0.5t to its equivalent P=P0 (b)t.

Note: P0 = 1.25 and b = e k =e0.5 = 1.6487 so formula needed is P=1.25(1.6487) t

Example 3 - Write a possible formula for the function shown in the table below:
 
N, number 11.25 25.3125 56.9531 128.1445
t, time in second 2 4 6 8

Solution: A check of the function does not show that it is linear, however a check of the ratio of successive to prior terms for
N with the same change in t, the independent variable, is a constant. So the function is exponential and as t increases N also
increases; this is an exponential increasing function of the form N=N0(1+r)t

(check of exponential -  )

Find 1+r or b: 

Now find N0: N=N0 (1.5)t , Using 3rd point (6, 56.9531) we get: 56.9531=N0 (1.5)6

, so Formula is N=5(1.5)t

Example 4 - Write a possible formula for the function shown in the graph below:
 
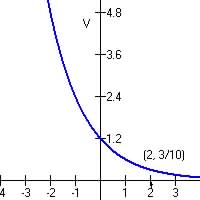It looks like an exponential decreasing function so of the form: V=V0(1-r)t

Note V0 = 1.2, so V=1.2(1 - r)t

One other point is given, (2, 3/10) so substitute in formula above to find 1 - r

, So 

, So formula is

V=1.2(0.5)t

Example 5 - The value of a special solar equipment depreciates in value according to an exponential model if at t = 5 its
value was $85,000 and at t = 8 its value was $26,500.

(a) Write a possible formula for the depreciation of the value of the equipment since t = 0.

(b) State the rate of depreciation in percent if t is time in years.

Solution

Note 2 points are given: (t, V): (5, 85000) and (8, 26500). Possible form of formula is V=V0(1-r)t

(a) Find 1- r: 

So 

Find b use one of the point say, (5, 85000): 85000 = V0 (0.6781)5 where 

So formula is V=592980.86(0.6781)t

(b) Since 1 - r = 0.6781, then r = 1- 0.6781 = 0.3219, its equivalent percent is 32.19%

So the rate of depreciation is 32.19% or decreases at a rate of 32.19% each year.

Example 6. State the balance of an orginal deposit of $35,000 in an investment account after 12 years
if the following rate of compounding is true:

(a) compounded yearly at a rate of 4.15%

Given r = 0.0415, t = 12, B0 = 35000 and rate of compounding is n = 1

Formula is: 

(b) compounded monthly at a rate of 5.25%

Given r = 0.0525, t = 12, B0 = 35000 and rate of compounding is n = 12

Formula is:

(c) compounded daily at a rate of 6%

Given r = 0.06, t = 12, B0 = 35000 and rate of compounding is n = 365

Formula is:

(d) compounded continuously at a rate of 5%

Given r = 0.05, t = 12, B0 = 35000 and rate of compounding is n = big

Formula is: