Example 1 - For the function  provide the following information:

(Note: You should be able to sketch any function and clearly show or state the information asked below)
 

(1) A sketch (see below)

(2) Regions where function is increasing (3) regions where function is decreasing (4) Point(s) where function have zero slope ( x = -2 and x = 1.5) (5) The y-intercept (when x = 0) is y = -9 (6) The x-intercept(s) (when y is 0) are x=-3, -1 and 3 (7) Value of function when x = -5 and x = 5 (a) y when x = -5 is -64 and 96 when x = 5

Example 2. If the price of gasoline is directly proportional to the number of gallon purchased and 5 five gallons cost $7.75,
how many gallons can $10 buy? (report answer to 2 decimal places) with the following properties:

Let G be gallons and C be cost for total gallon of sales, then

, Given G = 5 and C = $7.75, then 

So if C = $10 (money we have to buy gasoline), then we can buy 

We can buy 6.45 gallons with $10.

Example 3. If 12 machines can manufacture a widget in 30 minutes and the time it takes to manufacture
a widget is inversely proportional to the number of machines, how many machines are needed to
manufacture a widget in 1 hour and 30 minutes?

Let N be number of machines and H be the time to make one widget.

Then since H is inversely proportional to N, 

So when H =1.5 hr. or 90 minutes and k = 360, 

So 4 machines are needed to make 1 widget in 1 hour and 30 minutes.

Example 4. Identify graphs with the following properties:

(a) x is directly proportional to y (b) x is indirectly proportional to y

(c) y is inversely proportional to the square of x (d) y is directly proportional to the square root of x
 

(a) , e.g. y = x	(b)
(c)	(d)

Example 5. For the function y = x³ - 2, what is the rate of change of the function from x = 3 to x = 5?
 

The rate of change is  =  To 4 decimal places rate of change is 32.6667

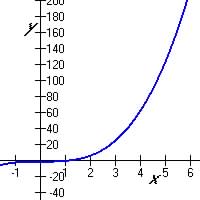Examples 6. In graduate school its cost $650 per credits and a semester registration fee of $50.

Write a formula that relates the Cost, C for taking (at least 1 credit per semester) N number of credits per semester.

Let C be total cost and N be number of credits.

Then C = $650(N) + $50, C = 650N + 50

Example 7. Sketch the following function and state following y = |2x - 3| - 2:
(a) the value of y when x = -5 and (b) the value of x when y = 5.
 

Sketch of Function (all sketches of functions should include where the function crosses the x and y axes and optimal points - maximum and minimum points within the window of the sketch - label all axes numerically for without the label the sketch is meaningless) (a) when x = -5, y = |2(-5) - 3| - 2 = |-10 -3 | - 2 = |-13| - 2 = 13 - 2 = 11 (b) when y = 5, x: 5 = |2x - 3| -2 5 + 2 = |2x - 3| = 7,  7 ) = 2x - 3 2x = 3  So  (x = -2 and 5)

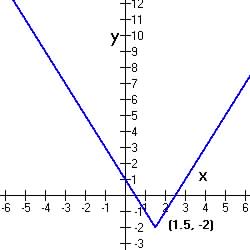If you do not understand how to work out these problems after seeing these example, see instructor prior to class.