Question 1 A quality engineer must sample a gold rod needed for a certain assembly unit.

(a) describe one random variable of possible interest

(b) Is the random variable discrete or continuous?

Solution

Volume (continuous) and Number of Defect (discrete)

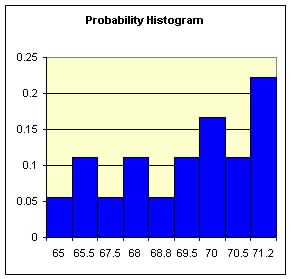
Question 2. The table shown is the yearly salary of 18 persons in a department in thousands of dollars:
 

65.0 65.5 65.5 67.5 68.0 68.0 68.8 69.5 69.5 70.0 70.0 70.0 70.5 70.5 71.2 71.2 71.2 71.2

Let x be the yearly salary, Find the probability distribution of x, and compute its mean and standard deviation.

Solutions

A Distribution of values can be written as:
 

Salary, x	65	65.5	67.5	68	68.8	69.5	70	70.5	71.2
frequency	1	2	1	2	1	2	3	2	4

Distribution -
 

The mean = 69.06 and standard deviation = 2.0011 is determined by group mean and variance formulas
 

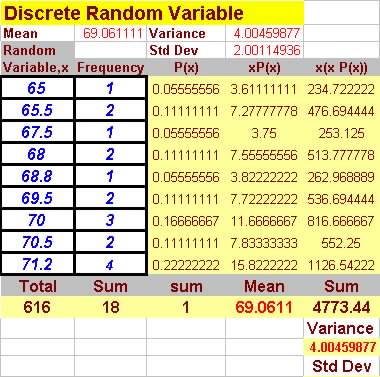Question 3. The following table shows the frequency of a discrete variable x.
Find its probability distribution and its mean and variance.
 

x	Frequency, f
10	130
20	130
30	70
40	80
50	40
60	10
70	20
80	10
90	10

Mean = 29.8 and standard deviation = 19.5438
 

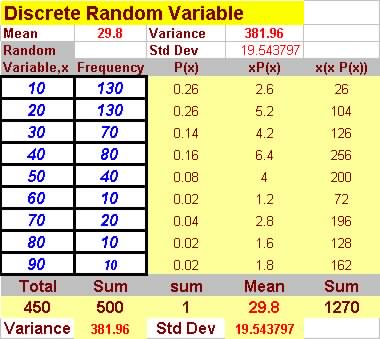Question 4. Below is the number of patients admitted to a small rural hospital last year and treated or
seen in one or more departments within the hospital. Find the mean, variance and standard deviation,
if x represents the number of departments each patient visited after admission.
 

Number of department visited, x	Number of Patients
1	30
2	150
3	30
4	15
Total	225

Solution - Mean = 2.13 standard deviation = 0.718
 

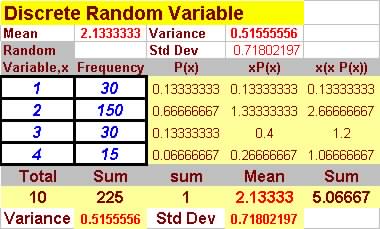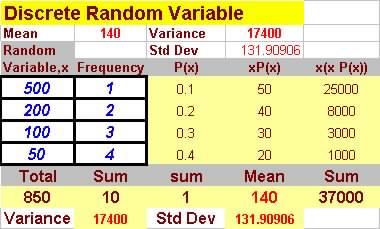
Question 5. A nonprofit organization plan to sell 1000 raffle tickets at $10 each to help with its annual fund raising campaign.
The campaign committee plans to give one prize of $500, two at $200, three at $100 and four at $50.
If you plan to buy one raffle ticket, what is your expected net winnings?
Note the probability of getting $500 is 1/1000, $200 is 2/1000, $100 is 3 in 1000 and $50 is 4/1000.
 

Winning, $	Frequency
500	1
200	2
100	3
50	4

Expected value is the mean = $140, You pay $10 and expects to win $140, so your net winning is 140 - 10 = $130
 

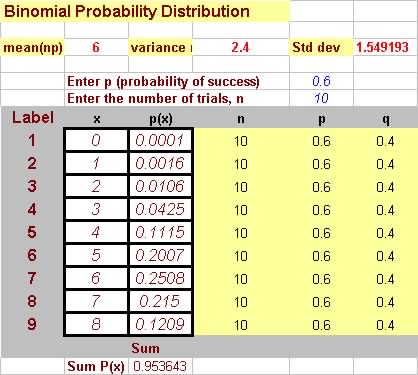
Question 6. Consider the binomial experiment with n= 10, p = 0.6, and x = number of successes.
Use the binomial distribution table to find the probability of:

(a) x less than 4

(b) x is greater than 6 and less than 8.

(c) x is greater than or equal to 6 and less than or equal to 8

(d) x is equal to 6.

(e) x is greater than 0

Solutions

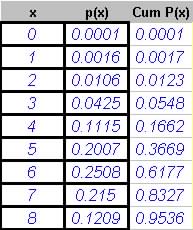
(a) Pr[x<4] = Pr[0] + Pr[1] + Pr[2] + Pr[3] = 0.0001 + 0.0016 + 0.0106 + 0.0425 = 0.0548

(b) Pr[6<x<8] = Pr[x<8] - Pr[x<6] = 0.8327 - 0.3669 = 0.4658

(c) Pr[6=<x=<8] = Pr[x=<8] - Pr[x=<6] = 0.9536 - 0.6177 = 0.3359

(d) Pr[x=6] = Pr[6] = 0.2508

(e) Pr[x=0] = 1 - Pr[0] = 1 - 0.0001 = 0.9999

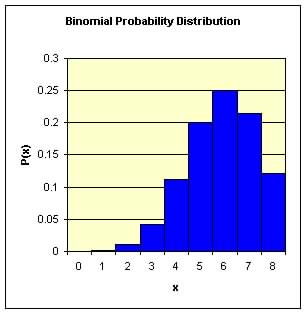
Binomial Distribution
 

Binomial Distribution
 

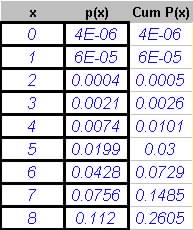
Question 7. 34% of voters opposed a proposed registration. If 30 voters are selected at random, find the probability that.

(a) 8 opposed the registration.

(b) More than 4 opposed the registration.

(c) Fewer than 6 opposed the registration.

Solutions: p=0.34, n = 30

(a) Pr[x=8] = 0.112

(b) Pr[>4] = 1 - Cum Pr[x<4] = 1 - 0.0101 = 0.9899

(c) Pr[x<6] = Cum Pr[x < 5] = 0.0.3
 

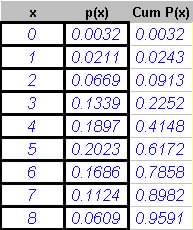
Question 8. 25% of students at City College have blood type O. In a random sample of 20 students, find the probability that:

(a) 1 will be type O.

(b) 2 or 3 will have type O.

(c) 1 or more will not have type O

(d) What is the approximate mean number of those sampled will be type O.

Solutions: p=0.25, n = 20

(a) Pr[x=1] = 0.0243

(b) Pr[2 or 3] = Pr[2] + Pr[3] = 0.0913 + 0.2252 = 0.3165

(c) Pr[1 or more] = Pr[None] = 1 - Pr[1 or more] = 1 - Pr[1=<x] = 1 - (1-0.0032) = 0..0032

Or Pr[None] = Pr[x=0] = 0.0032

(d) Expected value = np = 0.25 x 20 = 5
 

Question 9. Of the 5,600 patients admitted for treatment only 280 were black.
A sample of 100 patient records is to be selected at random. Let x be the number of blacks
and assume a binomial distribution. Find (a) the mean, (b) the variance and (c) the standard deviation of x.

Let p = 280/5600 = 0.05

Sample size is n = 100

(a) mean = np = 100 x 0.05 = 5

(b) variance = npq = 100 x 0.05 x 0.95 = 4.75

(c) standard deviation = sqrt(npq) = 2.1794