(a) Construct the frequency distribution.

(b) What percentage of recovery times were less than 10 days?

Solutions:

(a) The frequency distribution (the number of times each occurred) of each recovery times (range from 2 to 12) is:
 

Recovery Times, x	2	3	4	5	6	7	8	9	10	12	Total
Frequency, f	1	5	6	3	6	6	4	2	2	1	36

(b) Sum of frequencies up to and including 9 is 33 so percentage less than 10 is

Question 2. The owner of a small business wants to analyze the profits (thousands of dollars) over the past 30 years.
The ordered data from smallest to largest profits are as follows:
 

15	17	18	19	20	20	20	21	23	23	24	24	24	24	24
25	25	25	25	25	26	26	27	27	28	29	30	30	31	32

(a) Complete the grouped frequency distribution table:
 

Class	Class boundaries	Frequency
2	17.5-20.5

(b) What is the class width?
(c) Compute the relative frequency of each class
(d) What is the median and mode?

Solutions:

(a), (b) and (c) Relative Frequency table - Class width is 20.5 - 17.5 = 3
 

Class	Class boundaries	Frequency (1)	Relative Frequency (1) / (2)
1	14.5-17.5	2	0.667
2	17.5-20.5	5	0.167
3	20.5-23.5	3	0.1
4	23.5-26.5	12	0.4
5	26.5-29.5	4	0.133
6	29.5-32.5	4	0.133
Total		(2) Sum = 30	Sum =1

(d) The mode is 24 and 25 since they appears the most, 5 times

The median is (24 + 25) /2 = 24.5

Question 3 - The following is the world distribution of nuclear reactors in operation:
 

United States	109	Russia	29
France	56	Canada	21
Japan	51	Germany	20
United Kingdom	35	Others	116

(a) Construct a bar graph

(c) Construct a pie chart

Question 4. From the following data (per 1000 population) for selected countries:
Compute the statistics required for a box-plot diagram: Ordered Data
 

4.9	5.1	6.3	6.7	7	7.1	7.8	8.6	8.7	8.8
8.9	9	9.4	9.4	9.5	9.6	9.9	10	10.1	10.1
10.1	10.3	10.4	10.7	10.9	11.3	11.6	11.8	14.3

Solutions: (see programs)
 

min	25 percentile	median	75 percentile	max
4.9	8.6	9.5	10.3	14.3

Basic Statistics - Mean and Variance                         Enter Data         Basic Statistical Parameters 4.9 5.1 6.3 6.7 7 Sample,n 29   8.9 9 9.4 9.4 9.5 mean 9.251724138   10.1 10.3 10.4 10.7 10.9 std dev, s 2.040766783   7.1 7.8 8.6 8.7 8.8 variance 4.164729064   9.6 9.9 10 10.1 10.1 median 9.5   11.3 11.6 11.8 14.3   mode 10.1 Look for more           range 9.4             max 14.3             min 4.9                   Percentile     Box Plot   Inter quartile Range = 1.7 100% 14.3   Min 4.9 Semi-inter quartile range = 0.85 75% 10.3   25% Pt 8.6       50% 9.5   Median 9.5     25% 8.6   75% Pt 10.3       10% 6.62   Max 14.3

Question 5 The following grouped frequency distribution represents the ages (in years) of 59 patients of a counseling center.

(a) Compute a frequency polygon and

(b) Compute the mean and standard deviation of the age of the patients.
 

Class Limits	21-27	28-34	35-41	42-48	49-55	56-62	63-69
Frequency	3	7	12	15	12	7	3

Solution.
 

Class Limits	21-27	28-34	35-41	42-48	49-55	56-62	63-69
Class Midpoint	24	31	38	45	52	59	66
Frequency	3	7	12	15	12	7	3

(a) Frequency polygon

(b) Weighted Mean and Grouped Standard Deviations Weighted Mean = 45 Group variance = 113.2069 Group Standard Deviation = 10.64

Program Output

Question 6. The following data gives the average temperatures per month over a
12-month period for two cities A and B.
 

City A	8	14	25	43	54	64	71	69	58	47	29	16
City B	56	60	58	62	63	68	69	71	69	67	61	58

(a) Which of the two cities do you suspect is warmer on average? Which has more temperature variability?

(b) Use the following information and compute the mean and standard deviation for each city.

City A  and 

City B  and 
 

(a) City B has the larger mean of 63.5 And City A has a larger variation in temperature with a larger variance of 504.64

(b) From Formula: City A  and City B  and City A:  = 22.46 mean =  City B: mean = 63.5 and s=5.11 Variance = 26.09

Example of calculation for City B

Question 6 The following data give the time in days from remission to relapse for 51 patients with an acute illness.
 

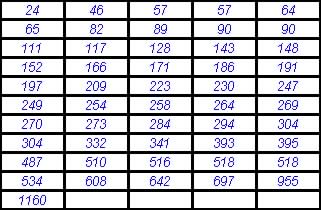Find the following:
 

Questions	Solutions from Program
(a) The first and third quartiles	135.5 and 367
(b) The inter quartile range	231.5
(c) The median	249
(d) The 95th percentile	669.5
(e) The percentile rank of 111	20%