Group A	Group B
Question 1a: Write a possible formula for the exponential function with these 2 points: Expects answer in the form: P=P0(b)t, where P0 and b are constants (a) Write formula: (b) When will P = 100?	Question 1b: Write a possible formula for the function shown in the table below:   V 6 54 486 4,374 t 1 3 5 7 (a) Write answer in the form: P=P0(b)t (b) How long does it take the function to double?
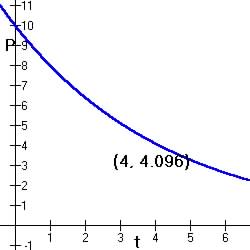
Question 2a. Write a possible formula for the  function shown below and State when  P = 1.  P = t = __________ when P =1	Question 2b. The number in attendance for the play  "Grapes of Wrath" per week seems to follow an  exponential function. If 200 patrons attended the 2nd week  and 150 patrons the 4th week. Write a possible formula for the number of patrons, N attending per week, t since the play was opened. Expect answers in form: N=N0(b)t     When did the number of patrons reached 100?

Question 3. When will  2 populations be equal in size if  Population 1 since 2003 expects to grow by the rules P1=200(1.025)t and Population 2 expects to grow by P2 =150(1.035)t  (Hint let P1 = P2) Expect answer in years (reported to 4 decimal places)

Question 4. When will any one of an investment of $50,000 after reach $1,000,000 if the annual interest rate is 6% and compounded either: (a) monthly (b) daily  or (c) Continuously