|
Construction of Quadratic Formula
To construct the Quadratic Formula you need either the Vertex and one
other points, or the Zeros and one or two other points, or three collinear
points.
To construct the formula from any representation of the quadratic model
one must be given the above and unless a graph is shown that models that
of a quadratic the problem should state of indicate that the model is quadratic.
The following three examples illustrate how a quadratic model can be
derived from a set of points:
Example 5.5.9 Find a quadratic formula given the following the vertex
is (2, 10) and a point on the graph at (6, 20)
Table 5.5.9 Quadratic Formula Given the Vertex and Another Point:
Since the Vertex is (2, 10) and the
other point is (6,20), the graph opens upward so a minimum whose model
is 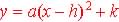
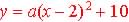 ,
Substitute (6, 20): ,
Substitute (6, 20):
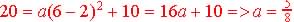
So quadratic Formula is

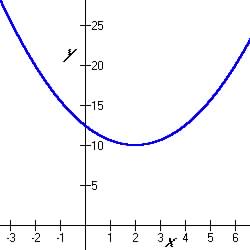
See Figure 5.5.12 to right |
|
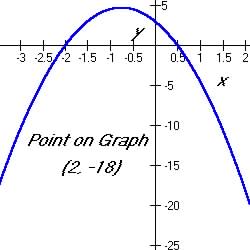
Example 5.5.10 Find a possible formula from the graph shown below:
Table 5.5.10 Quadratic Formula from the Zeros and another point:
| Figure 5.5.13
|
From graph there is a possible quadratic
maximum with zeros at x = ½ and -2 and a point at (2, -18):
So using Zero Form of the Model we get:
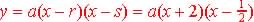
Use (2, -18) to find a:
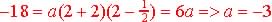
So possible formula is  or
or  |
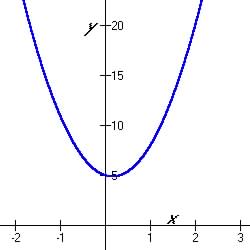
Example 5.5.11 Find the quadratic formula from given three non-collinear
points (0, 5), (1, 8) and 2, 20):
| Collinear
points are points in the plane that lie on the same common line.
If the 3 points are non-collinear then a plot of these points
would show that they are not on the same line so there exist a unique quadratic
formula whose graph passes through these points. |
Table 5.5.11 Quadratic Formula from 3 Non-Collinear
Points:
| Given the points (0, 5), (1,
8) and (2, 20)
From a quadratic model find the formula:
The points are non-collinear since they are not on common line. 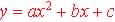
In order to find the coefficient a, b, c we need to solve
the system of linear equations:
(1) 
(2) 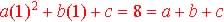
(3) 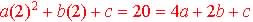
(2) a + b = 3
(3) 4a + 2b = 15
(2) a = 3 - b, So substitute in (3)
(3) 4(3 - b) + 2b = 15 = 12 - 4b + 2b, 
(1) 
So 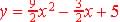 |
Figure 5.5.14
|
Precalculus: Contemporary Models
by Pin D. Ling
|