A Piecewise function is a function with a different formula for different parts of the domain of the function.

The Absolute Value Function is a defined Piecewise Function with the following formulas:

Table 3.4.1 The Absolute Value Piecewise Function
 

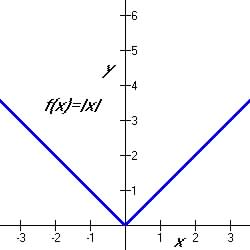Example 3.4.1 Another example of a Piecewise function:

Note that at x = 1 only the formula f(x)=x² applies. That is, for the formula f(x)=2x+1,
there is no value when x = 1 or less than 1; this is illustrated on a graph by a small circle or empty circle "o".

Often the Piecewise function is called a Defined Function since a different formula is defined for each domain.

Table 3.4.2 The graph of the Piecewise Function defined in Example 3.4.1 above.
 

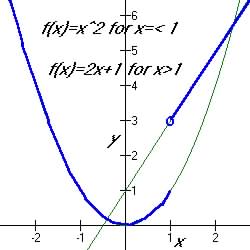For Domain of x equal to and less than 1  y=x2 and for Domain of x greater than 1 y=2x+1

Graphing Piecewise Functions:

Often it is best when graphing Piecewise functions to graph each formula on the same graph and then emphasize each
formula for the domain in which it is defined as shown in Table 3.4.2 above.

Make sure you note where each function exist or is defined by the presence of a solid line and where each function is not defined
by the present of an empty circle "o".

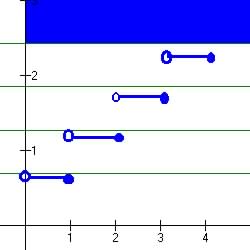
Example 3.4.2 Real World Example of a Piecewise function - A Word Problem.

The cost of a long-distance daytime phone call from Toronto to New York City is 69 cents for the first minute
and 58 cents for each additional minutes (or part of a minute).

Sketch the graph of the cost, C (in dollars) of the phone call as a function of time t (in minutes).

Table 3.4.3 Graph of a Step Function (Piecewise Function)
 

Let C(t) be the cost for t minutes. Since t > 0, the Domain of the function is  The Piecewise Function is then: Defined Function Domain C(t) = 0.69  C(t) = 0.69 + 0.58 = 1.27 C(t) = 0.69 + 2(0.58)=1.85 C(t) = 0.69 + 3(0.58)=2.43