The following table list the formula and key properties of the most of the functions discussed in this text: 
These formulas are often refer to as Mathematical Models:
 

Mathematical Models: The use of a function to represent a mathematical problem whether real or theoretical

Table 1.4 Types of Functions by Formula(s) and Properties: a, b, k, m, s, r, A, B, C, D are constants
 

Directly Proportional Models 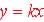, k is a constant 1 point can define function	Inverse Related Models , graphs have Vertical and Horizontal Asymptotes 1 point can define function	Absolute Value Models actually 2 functions: Domain Specific Linear Fcts.
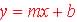
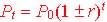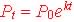Linear Models Rate, m is a constant value 2 points to define function The y-int at b	Exponential Models or or  The rate is in % (related to r) 2 points defines function	Exponential Money Models , r is yearly rate , y-int at
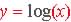
Logarithm Models Logs are the inverse of Exponential No value for function  If 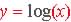 then its inverse	Piecewise Models Different functions for specified values (domains) for independent variable, x	Quadratic Models: Vertex Form:  Zero Form: Standard Form: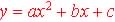 A polynomial with at most 2 zeros
Periodic Models: Cyclic fcts that repeats at constant intervals - periods Easily formulated from graph	Trigonometric Models: Law of Sines Law of Cosines Properties of Right Triangles Numerous Identities	Transformation of Functions: Given 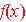 Transform
Inverse of Functions: Given: Find:	Polynomials:	Rational Models: 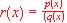p(x) & q(x) are polynomials (Asymptotes)

Click here for graphs of functions: