Proportions, Percent and Rate
of Change
Proportional Models:  or
or 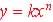 and :
and :  or
or 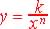
| A Direct
Proportional relationship is one which an increase in the input of
the independent
variable or attribute results in an increase in the output or dependent
variable or attribute by a
constant ratio called k, the constant of proportionality.
 or
or 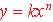 k and n are constants, n > 0
k and n are constants, n > 0
|
As x increases y also increases so we have an increasing function. Often
students need to observe the value of the function as x increases to find
clues as to the nature and parameters of a function.
The parameters are the constants values of a function that determine
its shape, slope, transformation, limits, and sketching boundaries. Some
parameters are natural occurring values such as 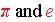 . .
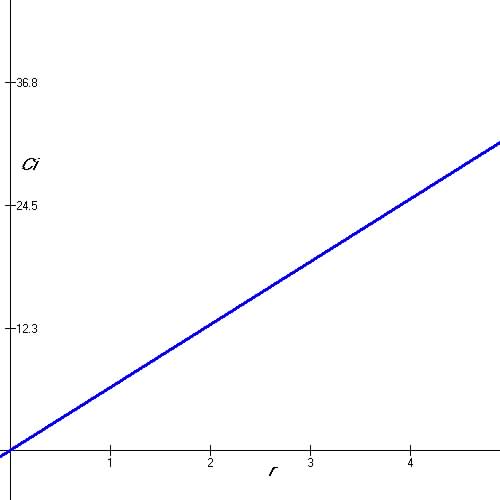
Table 1.5 Example 3 Directly Proportional Problem:
| Word Problem Statement: The
Circumference, C of a circle is directly proportional to the radius
of the circle, from the table of values find the formula for the Circumference
of a circle. |
Table of Values:
| Radius |
Circumference |
| 0 |
0 |
| 2 |
12.5664 |
| 4 |
25.2327 |
|
| Graph from Table: Figure 1.5
|
Formula from table or graph:
Since directly proportional: 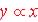
Or 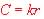 so so
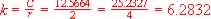
So formula is: C = 6.2832 r |
Note the key word or phrase (directly proportional) in the word
problem that identify the problems as a
direct proportional mathematical model. You should look of key word
or phrase when trying find the clues
that describe the type of mathematical model being considered.
| A Inverse
Proportional relationship is one which an increase in the input of
the independent
variable or attribute results in a decrease in the output or dependent
variable or attribute by a
constant ratio called k, the constant of proportionality.
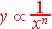 or
or 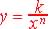 k and n are constants, n > 0
k and n are constants, n > 0
|
As x increases y decreases, so we have a decreasing function. This type
of function is also called a
Rational Function. Rational functions are characterized by functions
that contain asymptotes and holes.
| Asymptotes
are lines where the function tends to approach as values for the independent
variable becomes very large or very small.
Holes are regions or points where the function
does not exist (that is, no x or y values) |
Table 1.6 Example 4 Inverse Proportional Problem:
| Word Problem Statement: The
Population in thousands is inversely proportional to the square
of the time in years since 1985 and is given by values in the table on
right. Find a formula for the Population size, P with time, t. |
Table of Values:
| Time, t, years since 1985 |
Population in 1000 |
| 2 |
1.25 |
| 3 |
0.5556 |
| 4 |
0.3125 |
|
| Graph from Table: Figure 1.6

|
Formula from table or graph:
Since directly proportional: 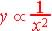
Or  so so
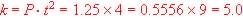
So formula is: 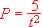 |
One set of points is needed to find the formula for proportional problems.
Percent:
Percent is a value that indicates
parts per hundred: 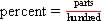
So 45% = 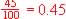
0.45 is the decimal equivalent of 45% |
In this text it is often required to convert percent to its decimal
equivalence and visa versa especially when we
work with exponential models. See learning module on Basic Math for
more about percents.
Rates and Rate of Change:
In a world were the only constant thing is change, the rate of change
becomes an important measure of how
fast or slow things are changing. Rates are proportions of two quantities
or the ratio of two attributes or variable that are changing.
| Rate is
the ratio of two variables or quantities, A and B that are changing and
is often stated as the ratio of the change in quantity A over the change
in quantity B. Sometimes the rate is referred to as the rate
of change and is model by:
Rate  |
Examples of rates includes:
Speed: rate of change of distance with time:  (55 mph)
(55 mph)
Population Growth: rate of change of population size with time:  (10,000 per year)
(10,000 per year)
Pay: rate of pay, $ with hours worked: 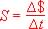 ($12 per hour)
($12 per hour)
Currency Exchange: rate of 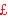 per $:
per $: 
Percent: parts per hundred: 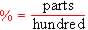
|