Shown below it simple illustrate that various inputs given a set of rules produced a predictable output.

Figure 1.1 Classical Model of a Function

For example, 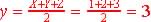: y is the function with the following rules: sum X, Y and Z and divide the sum by 2; so if X=1, Y=2, and Z=3, then the expected result or outcome would be equal to 3.

In this textbook we will explore many functions with specific set of rules and attributes that are characteristics of their unique mathematical models. With this understanding of functions one should become familiar with the rules that define specific functions (e.g. The absolute value function 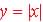 rules state that whatever the value of the variable x is - negative or positive - make it positive). One should also learn how to recognize the mathematical model that is best for a particular problems by examining the inputs and the content of the question being asked from the problems statement.

Example 1. What is the total cost of a $25 meal if the meal tax is 6% and the tip is 15%?

Step 1: Paraphrase the problem: Find total cost, C, $ for meal if taxes on meal of $25 is 6% and tips on $25 + taxes is 15%:

Step 2. Determine or find the values of the input and output variables and the Math Model that is suggested by the problem statement: Find Total Cost C, $, Given Price of Meal, P = $25 and the Tip is 15%, taxes is 6%. The Math Model suggested involves sums, products and ratios.

Step 3. Develop a Strategy to solve problem from information given or prior knowledge of similar problems. This problem requires an understanding of how tips and taxes are applied on a meal and the meaning of percent as related to the whole.

Step 2. Find an appropriate Representation of the Model - One could represents this particular problem with a formula: Cost = Price + tax + tip =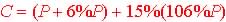 

Approach 1:

Or 

Approach 2:

C = (Price + 6% tax) + 15% of (Price + 6 % tax): 

Price = $25

6% Tax = $ 1.5 (0.6 x 25)

Price + Tax = $26.5 (25 + 1.5)

15%Tip = $ 3.975 (0.15 x 26.5)

Total Cost = Price + tax + tip = $25 + $1.5 + $3.975 = $30.475

See if you understand why both approaches 1 and 2 give the same result and are there other ways to solve this problem?

You will find many different ways to solve each problem presented in this textbook.

Properties of Functions:

A function must represents one or more relationships between two or more variables or attributes (weight, height, time, population size, investment balance etc.) The linear relationship between population size and time is a function.

A function must have only one output for each value of an input or combination(s) of inputs.

So to test if a graph is a function you draw a vertical line through the possible values of your input variable and there must be only one value for the function:  (x can be any value) is a function but 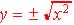 is not since there are 2 possible values for y for each value of x:

Table 1.1. Test for Functions - Vertical Line Test (there must only be 1 y value for the function for each value of x - Figures 1.2 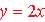 and Figures 1.3 )

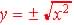is a function passes Vertical Line Test

Is not a function