| Introduction
The domain of a function are the possible values of x
that is defined by the function and the range are the possible values of
y
given the domain of the function.
Typically the range of a certain attribute is the difference between
the minimum and maximum values of that attribute. However, often the values
in between the range is not apart of the possible values of that attribute.
But we can use the typical concept of range to define the Domain as the
possible range(s) of the independent variable and Range as the range of
possible dependent variable. Because of this confusion of using range to
define Range and Domain; we will use the term Domain to refer to possible
independent variable and Range to refer to possible Dependent variable.
In problem solving the domain and range allow for designing functions
or math models or planning for or projecting possible outcomes of a function.
Often the domain is determined by constraints of the function and are know
ahead of time. For example if you are interested in a function, y
that describes the rule for the amount of paint needed to cover x
square footage of wall, the smallest square foot possible by the function
is 0 since the smallest area (square foot) one can cover is close to or
equal to 0. The maximum square foot for this problem will be determined
by the estimated total square foot of all the walls needed to be painted.
Do a possible domain would be for x = square foot: 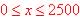 and to find the range one simple plug in the value of x = 0
in the function to find the smallest value of the Range and x = 2500
to find the largest value of the Range.
and to find the range one simple plug in the value of x = 0
in the function to find the smallest value of the Range and x = 2500
to find the largest value of the Range.
Example 3.1. Find the Domain and range for the following problem:
The cost in $ to coat n, square foot of aluminum is given
by the function 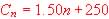 the maximum area to cover is 1,000 ft2.
the maximum area to cover is 1,000 ft2.
First find the Domain: The smallest area one can cover is 0 sq
ft and the maximum is given as 1,000 ft2.
So the Domain is  or [0, 1000].
or [0, 1000].
Then use the function 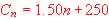 to find the Range: Smallest value of x is 0 so smallest value of y, the
range is
to find the Range: Smallest value of x is 0 so smallest value of y, the
range is 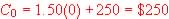 .
The largest value of x is 1000 so the largest value of y, the range is .
The largest value of x is 1000 so the largest value of y, the range is 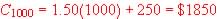 ;
So Range is ;
So Range is 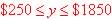 . .
Often both the domain are range are difficult to determine just the
problem statement alone. One must used algebraic, graphic or other means
to first determine the domain and then the range.
Given a function  ,
then the Domain of the function is a set
of values D, of x that are possible for the function. ,
then the Domain of the function is a set
of values D, of x that are possible for the function. |
Range
is a set of output values 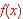 where x varies over the Domain of the function.
where x varies over the Domain of the function.
Range are possible values of y given the domain and the rule of the
function. |
|