Given a function , then the Domain of the function is a set of values D, of x that are possible for the function.

Range is a set of output values 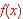 where x varies over the Domain of the function. Range are possible values of y given the domain and the rule of the function.

This chapter will discuss two approaches to find the Domain and Range of functions.

Algebraic and Graphic Approaches in Finding Domain and Range

Some formula or equation have unique or special characteristics that provides constraints that govern the Domain and Range of its function.

Square Root Function: 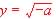(a is not a real number)

For the square root function we know that no real number a exist with a negative square root:

Example 3.2. Find the domain and range of the function :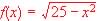

Algebraic Approach:

Since no real solution exist when  then 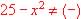 The content of the square root is negative only when  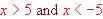so the Domain is .

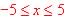The lower bound on the Range therefore is 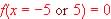 and observe as  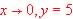its largest value. Here the Range is found by examining the extremes of the domain  and examining values of x that make maximum, so the Range is .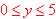

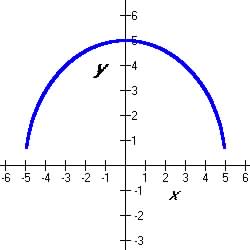
Graphical Approach:

A graph of the function shows the domain and range to match the algebraic conclusions.
 

Figure 3.3.1 Graph of :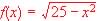

Example 3.3. Find the Domain and Range of the function: .
 

Algebraic Solution: Domain: 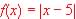. Looking at the function on see that all possible values of x are allowed, i.e. There are no mathematical restrictions as in the square root function: so Domain is all real numbers. However, the range is governed by the rules of the absolute value function that says all values in the |( )| be positive. But . So Range is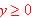

Figure 3.3.2 Graphic Solution: Supports the Algebraic

Example 3.4. Find the Domain and Range for 

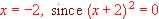
Algebraic Solution: The denominator cannot be = 0, since division by zero is not defined. But when denominator = 0 So the Domain of the Function is undefined at x= -2 So the Domain is all values of x except x = -2 (or  The Range, however is not so easily determined, one must examine the graph of the function and explore values of the function near and far from x = -2. Exploration shows that the maximum value of the function occurs when x = 0, or y = 0.5 So Range is

Figure 3.3.3 Graphic Solution  Shows a vertical asymptote at x = -2 (so Domain not defined there) and maximum value of y at x = 0, or y = ½ .

Some functions like a straight line, a quadratic equation and a exponential function have domains that are infinite or all possible real numbers for their x-values; however, close examinations of their graph or a study of the behavior of the function as x goes from large to small show these functions except the straight line to have restricted values of y or constrained Ranges.

There infinite variations to problems that address the question of find the Domain and / or Range of functions. It is best to first look for an algebraic solution and then a graphical one. Unless you are willing the explore the boundaries and intricacies of the graphic image in your calculator or graphing device, you may have some difficulties defining the true Domain and Range of the function. See the Challenge Problem for this section for an example.

Workshop on Finding Domain and Ranges of Functions: