Using Graphic Calculator to find Domain / Range:

Guide to finding domains (x-values) and ranges (y-values) using the Ti 85:
    1. Examine Function to see if Domain ( possible x-value ) is all real number, i.e. can be any positive or negative number
    2. Graphs the function in as big a window as possible and zoom in or out of graph
    3. Examine graph to see where function is disconnected for values of x
            If there is a vertical asymptote - then the function is not defined at that x-value(s)
            (plot graph in DrawDot Mode: [Graph] => [Format] => [DrawDot]
    4. Examine graph for one or more maximum and minimum for y-values:
            For minimums y >=  min value      for maximums   y < =  max. value
 
 

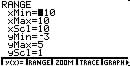
Example 1. Find the Domain and Range of : 
 

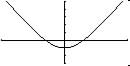        Domain: x  can be all real number
        Range: from graph there is a minimum value for y = -1 at x = 0, so range is y > = -1
                    Putting the value of x = 0 in the equation, y = -1, So y = -1 is real for this function
                    Since the function is not defined for y < -1, Range is y > = -1

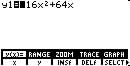
Example 2: the function h(t)  represents the height (in feet) of a ball above the ground for time t sec:

        h(t) = -16 t2 + 64 t
 

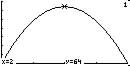        Domain: is the times in seconds between the ball being thrown and when it hits the ground i.e. y = 0:
                        Impose y minimum = 0 for that is the height of the ground
                        From graph:  Domain is 0 =<  x  =<  4
        Range: is minimum to maximum height, in feet:
                       From graph this is 0 =< y =< 64 , y = 64 when x = 2 sec
 
 

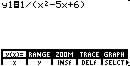
Example 3 Domain and Range Problems: y = 1 / (x2-5x+6)
 

DrawDot Mode

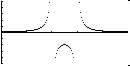
        Domain: From Graph there are two vertical asymptote: at x = 2 and x = 3

                   So f(x) is defined for: Domain of  all values of x except when x = 2 and x = 3

        Range: from Graph y is undefined for x = 2 and x = 3, y = - 4 at x = 2.5, So function is true for y = - 4
            However y is never = 0, it gets smaller with increasing or decreasing values of x but never = 0

            And the Range is; 

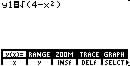
Example 4: Given Domain find Range: y = 

        (a) We must have 4-x2 >= 0, that is x2 =< 4, so the

            Domain of f(x) 

        (b)Plot y =
 
 

          

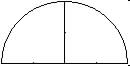        (c) Since 

Example 5 Domain and Range

        (a) m(x) = 9-x Domain all real numbers, x all real numbers

            Range all real numbers, y all real numbers
 
 
   

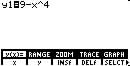
Example 6 y =  9 - x4 Domain all real number, x all real number
 
 

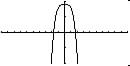            Since x4 > positive, largest value of y is when x = 0

            So m(x) =< 9 or Range is y =< 9

Example 7 : 
 
 
 


 

 


 
 

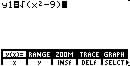
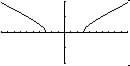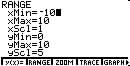
            So domain:  Range y(x) > = 0