Question 1 - Write the best formula for the graph shown below:

From Graph: Midline is D = -2.5

The amplitude is 2.5, the period is 2(6) = 12

So B =

Formula is: 

Question 2 Convert the following degrees to radians and state which quadrant each is in:

(a) -17 deg., (b) 400 deg.

(a) -17 deg = = -0.2967 rad Q-IV

(b) 210 deg = = 6.9813 rads Q-I (360 + 40)

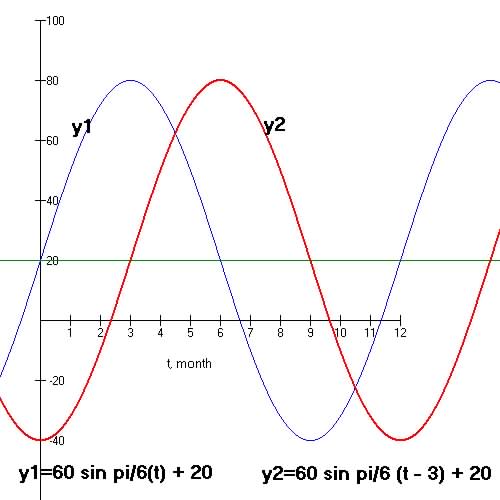
Question 3. 1 The lowest temperature on Hunter's Mountain, New York's premiere ski resort,
is -40 Deg Fahrenheit on Dec. 21 st (the 355 th day of the year), and the highest temperature
occurs on Jun. 21st and its 80 deg. Fahrenheit (the 172 nd day of the year). If a year has 366 days:

Temperature T(d) at day d is sinusoidal. (note time is in days or month)

(a) What are the mean, amplitude, and period for the function T(d)?

Given t = 355th day, h(t=355) = -40 Deg F and t =172 nd day, h(172) = 80 hrs

So maximum = 80, and minimum = -40: A =(80-(-40)) / 2 = 60 and D = -40+60 = 20

Since we go from a max to a min in 355-172 =183 days the from a max to a max is 366=P days.

B =

Mean = 20 deg F, amplitude = 60 and the period is 366 days

(b) Write a formula of Temperature as a function of time in days (or month), d.

So formula is

Question 4. The lowest temperature on Hunter's Mountain, New York's premiere ski resort,
is -40 Deg Fahrenheit on Dec. 21 st (the 355 th day of the year), and the highest temperature
occurs on Jun. 21st and its 80 deg. Fahrenheit (the 172 nd day of the year). If a year has
366 days or 12 months:

Temperature T(d) at month d is sinusoidal. (note time is in months or days)

(a) What are the mean, amplitude, and period for the function T(d)?

Given t = 12th month, h(t=12) = -40 Deg F and t =6 th month, h(6) = 80 hrs

So maximum = 80, and minimum = -40: A =(80-(-40)) / 2 = 60 and D = -40+60 = 20

Since we go from a max to a min in 12 - 6 = 6 months the from a max to a max is 12=P days.

B =

Mean = 20 deg F, amplitude = 60 and the period is 12 months

(b) Write a formula of Temperature as a function of time in months, d.

So formula is

Question 5. Find the (x, y) coordinate that corresponds to the a point on a circle
of radius r = 3.5 cm and an angle of 0.75 rad. (use rads mode or convert to degree)

So (x, y) = (-2.4749, 2.4749) in Q-II

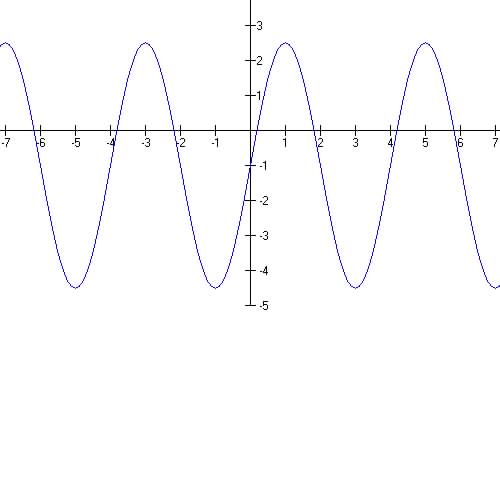
Question 6 - Write the best formula for the graph shown below:
 

From Graph: Midline is D = -1.0

The amplitude is 3.5, the period is 3 + 1 = 4

So B =

Formula is:

Question 7 Convert the following angles to degrees and state which quadrant each is in:

(a) -1.7 rads, (b) 3.1 rads.

(a)  = 97.4028 deg - Q-II

(a)  = 177.6169 deg Q-II

Question 8 The Confused Scientists Problem: A population of killer bees migrating
inland north towards a certain Texas city was estimated by a team of scientists and
their results are shown in the table below: Another group of scientists believes that
the migrated bees population growth is a sinusoidal model
 

Months after Migration	Estimated Population (thousands)
1	150 (first minimum)
5	2,400 (first maximum)

Write a formula for the model (hint use time in months)

Given t = 1 months, P(t=1) = 150 and t =5 months, P(5) = 2400

So maximum = 2400, and minimum = 150: A =(2400-150) / 2 = 1125 and D = (2400+150)/2 = 1275

Since we go from a min to a max in 4 months the from a min to a min is 8 months=P.

B =

So formula is  (the actual graph is shifted to the right by 3)

i.e. 

Question 9. Find the (x, y) coordinate that corresponds to the a point on a circle
of radius r = 12 inches and an angle of -45 deg.

So (x, y) = (8.4853, -8.4853) in Q-IV

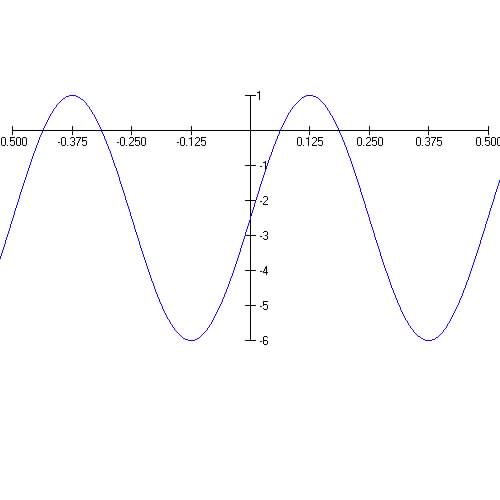
Question 10 - Write the best formula for the graph shown below:

From Graph: Midline is D = -2.5

The amplitude is 3.5, the period is 0.375 + 0.125 = 0.5

So B =

Formula is: 

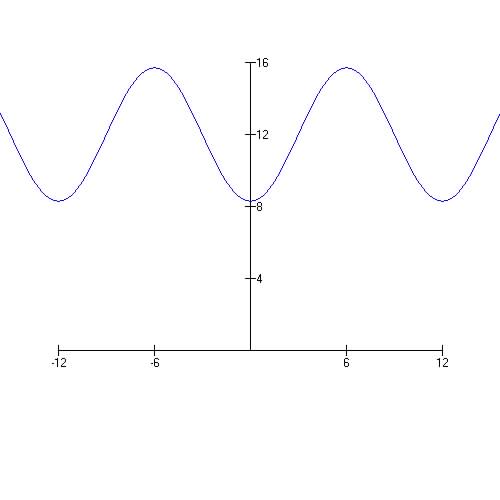
Question 11. Assume that the hours of daylight in Maine is given by a sinusoidal function d(t) of time.
During 1994, assume the longest day of the year is June 21 with 15.7 hours of daylight and the
shortest day is December 21 with 8.3 hours of daylight. Find a formula d(t) for the number
of hours of daylight on the t-th month of the year.

Given t = 6 months, h(t=6) = 15.7 hrs and t =12 months, h(12) = 8.3 hrs

So maximum = 15.7, and minimum = 8.3: A =(15.7-8.3) / 2 = 3.7 and D = 15.7-3.7 = 12

Since we go from a max to a min in 6 months the from a max to a max is 12 months=P.

B =

So formula is  (shifted 3 months to the right  )
 

(formula is actually  )

Question 12 Convert the following angles to degrees and radians:

(a) -5.1 rads to deg, (b) 210 deg to rads.

(a)  = 293.80 deg

(b) 210 deg = = 0.3491 rad

Question 13. Find the (x, y) coordinate that corresponds to the a point on a circle of radius,

r = 3.5 cm and an angle of 210 deg.

So (x, y) = (-3.0311, -1.75) in Q-III