(b) if ln(x) = y, then e y = x
Note x > 0 (i.e. ![]() )
in both graphs and
)
in both graphs and
When x = 1, y = 0
So ln(1) = log(1) = 0
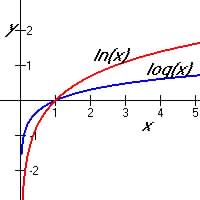
Each is the inverse function of the other.
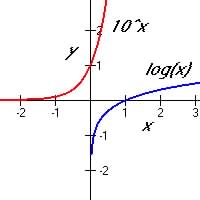
Each is the inverse function of the other
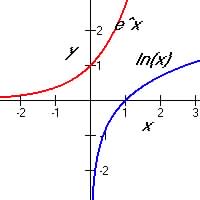
|
Theory |
by Example Series Applications of Logarithms |
Compare these two functions and state how they are related to exponential functions: y = log(x) and y = ln(x)
Example 2
Solve for t in the exponential functions: (a) 12=3(1.05) t and (b) ½ =3(0.85) t
| (a) 12=3(1.05) t
So |
(b) ½ =3(0.85) t
So |
| (a) Graphic Solution to 12=3(1.05)
t
|
(b) Graphic Solution to ½ =3(0.85)
t
|
Example 3
When will an investment of $200,000 reach $1,000,000 if it is invested
in an fund account that is compounded daily
at an annual interest rate of 6%?
| Algebraic Solution
So balance, B of the account after t years is:
So to find when Use logs to solve for t:
|
Graphic Solution
|
Example 4
How long would it take the number of microorganisms to double in a jar if the number is growing at a rate of 14.5% each hour?
| Algebraic Solution
Since exponential growth: Number doubles when
Therefore |
Numeric Solution
Let initial number be 25, then
Therefore Check |
Example 5
When will the population size of two populations be equal if population
A grows from 25,000 at a rate of 0.8% each year
and population B grows from 20,000 at a rate of 0.9% each year?
| Algebraic Solution
Let PA = PB: Group like terms: Note: :
|
Graphic Solution
|
Example 6
Solve for x in the following; (a) 2 = log(x-3) and (b) 6 = ln(104 + x)
| (a) 2 = log(x-3)
Since when y = log(x),
Check: log(103 - 3) = log(100) = 2 So x = 103 |
(b) 6 = ln(104 + x)
Since when y = ln(x),
Check: ln(104+299.4288) = 6 So x = 299.4288 |
Example 7
Solve for x in the following: (a) 1 = log(x-2) + log(x+2) and (b) 2 =ln(10x) - ln(x+2)
| (a) 1 = log(x-2) + log(x+2)
Properties: So 1 = log[(x-2)(x+2)]=log(x2 - 4) 1 = log(x2 - 4) Since when y = log(x), 101 =x2 - 4, So x2 = 10 + 4 = 14, Check: So |
(b) 2 =ln(10x) - ln(x+2)
Properties: So Since when y = ln(x),
Group like terms:
Check: ln(56.6) - ln(5.66 + 2) = 2 |
Example 8
Evaluate the following algebraically:
(a) Find x if log(x)=ln(x) (b) log(10,000) (c) log(0.001)
(d) lne3x+2 (e) log(10) - log(0.01) (f) 10log100
| (a) Find x if log(x)=ln(x)
The only time both functions are equal is when x = 1 So log(1) = ln(1) = 0 See Graph above |
(b) log(10,000)
Note 10,000 = 104 Since log 10x = x Then log 104 = 4 |
(c) log(0.001)
Note Since log 10x = x Then log 10 -3 = -3 |
| (d) lne3x+2
Since ln ex = x Then lne3x+2 = 3x + 2 |
(e) log(10) - log(0.01)
Note: log 10 = 1, log 0.01=-2 Also: So log(10)-log(0.01)=1-(-2)=3 |
(f) 10log100
Note log 100 = log 102 = 2 So 10log100 = 102 = 100 Therefore: 10log100 = 100 Also 10log(x) = x |